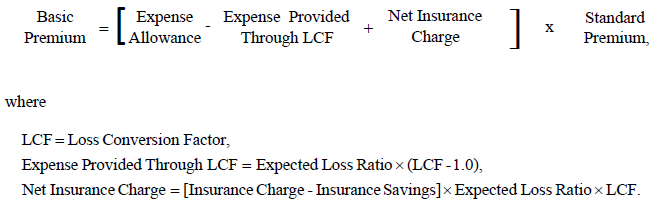Werner16.ClaimsMade

Reading: BASIC RATEMAKING, Fifth Edition, May 2016, Geoff Werner, FCAS, MAAA & Claudine Modlin, FCAS, MAAA, Willis Towers Watson

Chapter 16: Claims-Made Ratemaking

Pop Quiz

What is the formula for basic premium when calculating the premium for a retrospectively rated policy Click for Answer 

Study Tips

VIDEO: W-16 (001) Claims-Made Policies → 5:00 Forum

Questions on claims-made policies are some of the easiest points on the exam. This topic shows up on the exam about half the time and you can cover the material in less than a day. Just read the wiki article once or twice and do the old exam problems. The calculations are very easy once you understand the basic background information and concepts and the only thing you have to memorize is the 5 principles of claims-made policies.

Estimated study time: ½ day (not including subsequent review)

BattleTable

Based on past exams, the main things you need to know (in rough order of importance) are:

• calculate loss costs - for claims-made and occurrence policies
• 5 principles - claims-made policies

reference	part (a)	part (b)	part (c)	part (d)
E (2019.Fall #4)	policy cost - clms-made vs occurrence	rate adequacy - clms-made vs occurrence	other differences - clms-made vs occurrence
E (2018.Fall #4)	calculate loss costs - clms-made policy	calculate loss costs - occurrence policy	rate adequacy - clms-made vs occurrence	(d) reserve adequacy (e) investment income
(2018.Spring #6)	Excel Practice Problems
E (2017.Fall #4)	calculate loss costs - clms-made vs occurrence	calculate loss costs - clms-made → occurrence
E (2016.Fall #3)	calculate loss costs - occurrence policy	calculate loss costs - clms-made policy	reserve adequacy - occurrence → clms-made	target U/W profit - occurrence → clms-made
E (2016.Spring #5)	calculate loss costs - clms-made → occurrence	ultimate loss estimates - volatility	investment income clms-made vs occurrence
E (2015.Spring #7)	calculate premium - clms-made → occurrence	premium comparison - clms-made → occurrence	premium adjustments - law change
E (2013.Spring #6)	IBNR components - clms-made → occurrence	premium comparison - clms-made → occurrence	change in trend - clms-made → occurrence	(d) switch: occurrence → clms-made (e) switch: clms-made → occurrence

Full BattleQuiz

In Plain English!

Introduction

Werner has a good 1-page introduction to claims-made policies. Here's the direct link:

WERNER: Intro to Claims-Made Policies

The quiz has a few easy questions based on the introduction:

mini BattleQuiz 1

Report Year Aggregation

We covered report year aggregation way back in Reserving - Chapter 3 - Organizing the Data. There are 4 basic ways to organize actuarial data:

• CY or Calendar Year
• AY or Accident Year
• PY or Policy Year
• RY or Report Year

We noted that RY triangles work well for claims-made policies like professional liability. One of the main advantages of RY data is that by definition there is no pure IBNR, only IBNER, (Incurred-But-Not-Enough-Reported.) Since pure IBNR can be significant, using RY instead of AY triangles greatly reduces the risk of reserve inadequacy. This is Principle #4 which is explained further down. There are 5 general principles related to claims-made policies.

Here is the example we'll use to demonstrate the 5 principles. It's essentially the same example as in the text but without the decimal places. The tables are the same except for color-coding and the totals in the last column.

• The table on the left highlights entries on a row that sum to the total loss costs for report year 2020.
• The table on the right highlights entries on a diagonal that sum to the total loss costs for accident year 2020.

(The loss costs in the last column of each table might not exactly equal the sum of the appropriate entries in the triangle due to rounding, but it was easier on my eyes not to show the extra decimals.)

Here's how we refer to entries in this table:

• L(2020, 0) = 200 = Loss costs for RY 2020 with lag 0
• L(2020, 1) = 200 = Loss costs for RY 2020 with lag 1
• L(2021, 0) = 210 = Loss costs for RY 2021 with lag 0

Pop Quiz A: If L(Y, 3) = 255 then what is the value of Y. Click for Answer 

Here's how we interpret entries in the tables. Refer to the blue entries in the table on the right.

• L(2020,0) = 200 corresponds to claims reported in 2020 with a lag time of 0

→ this means the claims occurred in year 2020 - 0 = 2020 (in other words, the accident year was 2020)

• L(2021,1) = 210 corresponds to claims reported in 2021 with a lag time of 1

→ this means the claims occurred in year 2021 - 1 = 2020 (in other words, the accident year was 2020)

Both entries are in the same accident year and in general, accident year equals report year minus lag. The total loss costs for accident year 2021 is the sum of the entries L(Y,i) where Y-i = 2021:

• accident year 2021 occurrence policy loss costs

= L(2021,0) + L(2022,1) L(2023,2) L(2024,3) + L(2025,4)

= 210 + 221 + 232 + 243 + 255

= 1,161

It should really total 1,160 but that's just rounding because the entries in the table are displayed only to the nearest integer. You should quickly verify the occurrence loss cost totals for the remaining years.

The interpretation of the beige entries highlighted in the table on the left is very easy.

• all entries in the row correspond to claims that were reported in 2020 even thought these claims occurred in different years:
• L(2020,0) occurred in 2020 - 0 = 2020
• L(2020,1) occurred in 2020 - 1 = 2019
• L(2020,2) occurred in 2020 - 2 = 2018

It's very important that you understand the relationships between report year, lag time, and accident year. This example also made a few simplifying assumptions:

• Exposure levels are constant.
• The average loss cost for Report Year 2020 is $1,000.
• Loss costs increase by 5% each report year.
• An equal number of incurred claims are reported each year and all claims are reported within five years of occurrence (i.e., 20% reported each year).
• Loss costs do not vary by report year lag. Also, any trends affecting settlement lag have been ignored.

We use this simplified example to demonstrate the 5 principles below. (Note that these principles remain valid even without these simplifying assumptions.)

Principles

Ian-the-Intern gave green labels to principles 1-4 and a red label to principle 5. Can you figure out why? He will tell you in the summary at the end.

Principle 1: Loss Costs

1   A claims-made policy should always cost less than an occurrence policy as long as claim costs are increasing.

claim costs increasing  ⇒  cost(CM) < cost(Occ)

• If you look at the example, it's obvious why this is true. Claims-made yearly totals are sums of rows while occurrence policy totals are sums of diagonals. So if loss costs increase as you go down the table, the diagonal sum must obviously be greater than the corresponding row sum.

• Note also how pricing risk is significantly reduced with claims-made policies. Occurrence policies require projections from occurrence of claims (which is the policy trigger) to report, and then from report to settlement. In contrast, claims-made policies only require projections from report (which is the policy trigger) to settlement, and short-term projections are more accurate than long-term ones. Thus pricing risk is reduced.

Principle 2: Trends

2   If there is a sudden, unpredictable change in the underlying trends, the claims-made policy priced based on the prior trend will be closer to the correct price than an occurrence policy based on the prior trend.

sudden unpredictable change in trend  ⇒  accuracy(CM pricing) > accuracy(Occurrence pricing)

• If you look at the original tables with the 5% loss cost trend as you go down the columns, you'll see that for 2021, the claims-made loss costs are 1,050 while the occurrence loss costs are 1,160.
• Suppose however the loss trend suddenly and unexpectedly increases from 5% to 10% at the beginning of 2021. The revised table of loss costs is as shown below. Under this higher growth scenario, the claims-made costs for 2021 are 1,100, higher than the original projection of 1,050 by (1,100 / 1,050) = 4.7%. But the corresponding difference for the occurrence policy is (1,343 / 1,160) = 15.8%. In other words, the occurrence policy would now be underpriced by 15.7% versus the claims-made policy which is underpriced by only 4.8%.

Principle 3: Reporting Pattern

3   If there is a sudden, unexpected shift in the reporting pattern, the cost of a mature claims-made policy will be affected relatively little, if at all, relative to the occurrence policy.

sudden unexpected shift in reporting pattern  ⇒  effect on cost(mature CM) ~ 0 < effect on cost(Occ)

• To demonstrate this, let's shift the reporting pattern like this: Instead of the reporting pattern being uniform:

→ 20%, 20%, 20%, 20%, 20%,

• let's shift 10% of the claims are reported one year later than expected, but all claims are reported within five years. This new reporting pattern is:

→ 10%, 20%, 20%, 20%, 30%

• The effect of this change is shown below: There is no change in the claims-made total of 1,050. It's true that the first entry for 2021 is lower (105 versus the original value of 210) and the last entry is higher (315 versus 210) but these differences cancel each other out so the row total is the same: 1,050. This is not true for the occurrence policy however. The first and last entries in the diagonal sum do not cancel each other out. The first entry, 105, is lower than the original entry of 210 by 105, but the last entry, 383, is higher than the original entry of 243 by 140. The final occurrence loss costs for 2021 under the new reporting pattern are then higher by 140-105 = 35. The overall percentage difference is 1,183/1,160 = 1.98%.

Principle 4: Reserve Adequacy

4   Claims-made policies incur no liability for IBNR, so the risk of reserve inadequacy is greatly reduced.

pure IBNR(CM) = 0  ⇒  lower risk of reserve inadequacy

• The sequence of events with an occurrence policy is: occurrence of event → reporting of event to insurer → settlement of claim by insurer. The gap between occurrence and report relates to pure IBNR while the gap between report and settlement relates to IBNER. For claims-made policies however, the gap between occurrence and report is not relevant because coverage isn't triggered until report. That means pure IBNR = 0 and you only have to estimate the smaller quantity IBNER. When you estimate a smaller quantity, the risk of misestimation is lower.

Principle 5: Investment Income

5   The investment income earned from claims-made policies is substantially less than under occurrence policies.

Investment Income(CM)  <<  Investment Income(Occ)

• Investment income is earned by investing reserves, including unearned premium reserves, case reserves, IBNR reserves, and IBNER reserves. A claims-made policy has no (pure) IBNR to invest but also shortens the period of time between collection of premium and payment of claim so there's less time for investment income to accrue.

mini BattleQuiz 2

Determining Rates

There is nothing to learn in this section. The text states that once you've got the loss costs for a claims-made policy, the rate can be determined using the same methods as for occurrence policies from earlier chapters. Note that in earlier chapters we didn't specifically refer to the policies as occurrence policies – it was just assumed.

Coordinating Policies

Intro

This section is where many of the old exam problems come from. For various reasons, a professional liability policyholder may need to switch from an occurrence policy to a claims-made policy or from a claims-made policy to an occurrence policy.

Question what issues may arise when switching from a claims-made to an occurrence policy and vice versa

• there may be coverage gaps or coverage overlaps

(a coverage gap means the policyholder is unprotected, while a coverage overlap means the policyholder is paying twice for the same coverage)

Switching: Occurrence Policy to Claims-Made

As an example, consider a situation where a policyholder had purchased occurrence policies for several years all the way through to 2020, then switched to claims-made policies from 2021 to 2025. The cells where coverage was provided by these occurrence policies are indicated by the grey diagonals shaded grey. Starting in 2021, the policyholder switched to claims-made coverage, indicated by the cells across rows outlined in red.

• left-hand diagram: with coverage overlap (cells that are both inside a red box and shaded grey represent coverage overlaps)
• right-hand diagram: coverage overlap has been resolved by applying retroactive dates to the claims-made policies

→

Question how can coverage overlap be addressed when switching from occurrence to claims-made coverage

• give claims-made policies a retroactive date

→ claims-made coverage only covers claims that occur on or after the retroactive date

Remember that the year of occurrence is calculated as Y-i for the entry L(Y,i) in the table above. In other words: (report year) - (lag). Anyway, let's apply retroactive dates as follows:

• RY 2021: retroactive date = Jan 1, 2021

→ this means any claims that occurred prior to Jan 1, 2021 are not covered by the new claims-made policy

→ in the diagram, this refers to cells in the RY 2021 row where Y-i ≤ 2020

→ this would be cells L(2021,1), L(2021,2), L(2021,3), L(2021,4)

→ these cells correspond to claims that occurred respectively in 2020, 2019, 2018, 2017 (prior to Jan 1, 2021, so are not covered thus coverage overlap is avoided)

• RY 2022: retroactive date = Jan 1, 2021 (same as RY 2021 because that's when the switch from occurrence to claims-made policies was made)
• RY 2023: retroactive date = Jan 1, 2021 (same as RY 2021)
• RY 2024: retroactive date = Jan 1, 2021 (same as RY 2021)
• RY 2025: retroactive not relevant (we assumed the maximum lag was 4 so there would be no claims past lag = 4 for the RY 2025 row anyway)

The right-hand diagram above is redrawn incorporating the retroactive dates into the claims-made policies. There is no longer any overlap between the claims-made coverage and the occurrence policy coverage.

The claims-made policy for RY 2021 with the retroactive date of Jan 1, 2021 is called a first-year claims-made policy. Similarly, the subsequent claims-made policies are second-year, third-year, fourth-year, and mature claims-made policies. The mature claims-made policy no longer requires a retroactive date because the occurrence policies have stopped providing coverage. (Remember that in our example, we assumed the maximum lag was 4. None of the prior occurrence policies can be triggered past that point so they no longer provide any coverage that could overlap with the claims-made policies.)

The last thing to mention here is pricing adjustments for n^th year claims-made policies. A first-year claims-made policy obviously provides less coverage than a mature claims-made policy so it should cost less. We need to perform an analysis to determine the distribution of costs across each of the lags of a mature claims-made policy. Suppose the RY 2025 in previous example has the following losses:

• L(2025,0) = 400
• L(2025,1) = 700
• L(2025,2) = 850
• L(2025,3) = 950
• L(2025,4) = 1,000

From this, we can develop a potential step factor pricing structure for a claims-made policy:

claims-made year	step factor
first	40%
second	70%
third	85%
fourth	95%
mature	100%

The table implies that 40% of the costs of a mature claims-made policy come from claims that occurred and were reported during that year, 70% of the costs come from claims that occurred during that year and one year prior, and so on.

Switching: Claims-Made Policy to Occurrence

In this example, we make the switch in the opposite direction from the previous example. Consider a situation where a policyholder had purchased claims-made policies for several years all the way through to 2020, then switched to occurrence policies from 2021 to 2025. As before, cells shaded grey represent occurrence policy coverage and cells outlined in red represent claims-made coverage. The diagram on the right also has cells outlined in blue which represent tail coverage to fill in coverage gaps.

• left-hand diagram: with coverage gaps
• right-hand diagram: coverage gaps have been resolved with tail policies outlined in blue

→

Question how can coverage gaps be addressed when switching from claims-made to occurrence policies

• insurer provides tail policies

→ covers claims that occurred before Jan 1, 2021 but were reported after Jan 1, 2021

→ note that the latest claims-made policy would have expired on Dec 31, 2020 so claims reported after that date would not have been covered

Summary

Ian-the-Intern is just bursting to tell you why principles 1-4 have green labels and principle 5 has a red label! Principles 1-4 state differences between claims-made and occurrence policies that generally favor claims-made policies. Principle 5 on investment income is the only one where claims-made policies are generally worse

Exam Problems

Problems back to 2018: (not including TBE)

mini BattleQuiz 3

Problems from 2016-2017:

mini BattleQuiz 4

Problems from 2013-2015:

mini BattleQuiz 5

All quiz problems:

Full BattleQuiz

POP QUIZ ANSWERS

There are many terms in the formulas for calculating retrospective premium:

• Basic Premium: provides for

- insurer's U/W profit & expenses, excluding expenses provided for by the LCF (Loss Conversion Factor) and Tax Multiplier

- cost of limiting the retrospective premium to be between the minimum and maximum premium

- the formula for the basic premium is the most complicated part of this problem. You'll see how this works in the example further down.

Go back

Pop Quiz - A

• Y = 2025

Go back