Werner05.Premium

Reading: BASIC RATEMAKING, Fifth Edition, May 2016, Geoff Werner, FCAS, MAAA & Claudine Modlin, FCAS, MAAA Willis Towers Watson

Chapter 5: Premium

Pop Quiz

Is it possible for a calendar year to have negative written exposures? What about a policy year? Click for Answer

Study Tips

VIDEO: W-05 (001) Premiums → 8:00 Forum

This is a long chapter and it is very important. The source text explains most topics well and BattleActs supplements the theory with 8 web-based practice problems. (I found the sections on premium trending a little confusing however so I tried to approach that a little differently from the text.) It is very important that you become proficient in calculations involving:

the parallelogram method - calculating Earned Premium at Current Rate Level
premium trending - both 1-step and 2-step versions

Those are foundational skills for being able to calculate rate changes in Chapter 8 - Indications. Topics of somewhat lesser importance are the extension of exposures method for calculating earned premium at current rate level and premium development. You can't ignore those topics - just make sure to allocate your time and effort accordingly.

Exam questions also often ask you to comment on the advantages and disadvantages of each method but that's very easy to learn. Spend the bulk your time on the web-based practice problems as well as old exam problems. You may feel like you're getting bogged down in this chapter but it's time well spent. And remember, you can return any time you want for more practice.

Estimated study time: 1 week (not including subsequent review time)

BattleTable

Based on past exams, the main things you need to know (in rough order of importance) are:

parallelogram method - calculating current rate level factors (on-level factors), advantages / disadvantages
aggregating premiums by CY and PY
extension of exposures method
premium trending

reference	part (a)	part (b)	part (c)	part (d)
E (2019.Fall #2)	CYWP: - calculate ²	in-force premium: - calculate	CYWP: - calculate	(d) EP estimate using IFE (e) uses of IFE
E (2019.Spring #2)	parallelogram method - trended EP @ CRL	premium trend, CRL - effect of policy term
E (2018.Fall #2)	CYEP - calculate	PYLR - calculate
E (2018.Fall #3)	parallelogram method - on-level factor	extension of exposures - on-level factor	parallelogram method - appropriate? ¹
E (2017.Fall #1)	premium trend: - 2-step trending	negative premium trend: - give examples
E (2017.Fall #2)	parallelogram method - trended EP @ CRL	rate change: - method not specified
E (2017.Fall #3)	CYEP, CYWP - calculate	PYEP, PYWP - calculate	CY aggregation: - ads & disads
E (2017.Spring #2)	parallelogram method - EP @ CRL (PYs)	Werner07.OtherExpenses	parallelogram method - appropriate?	PY premium - change after PY end
E (2016.Fall #2)	parallelogram method - on-level premiums	parallelogram method - weaknesses
E (2016.Spring #2)	CYWP: - calculate	CYEP: - calculate	in-force premium: - calculate	CYEE: - by territory
E (2015.Fall #1)	CYWE, CYEE: - calculate	parallelogram method - on-level premiums	extension of exposures - on-level premiums
E (2015.Spring #4)	parallelogram method - trended EP @ CRL
E (2015.Spring #5)	parallelogram method - on-level premiums	parallelogram method - with uneven writings ³	alternate on-level method - suggest a method
E (2014.Fall #2)	CYEP: - calculate	CYWP: - calculate	PYEP: - calculate	PYWP: - calculate
E (2014.Fall #3)	parallelogram method - pros / cons	extension of exposures - pros / cons
E (2014.Spring #1)	parallelogram method - on-level factor	parallelogram method - uneven exposures	parallelogram method - 2-year policies
E (2013.Fall #2)	extension of exposures - on-level factor
E (2013.Spring #2)	premium trend: - 1-step trending	premium trend: - purpose	premium trend: - possible issues	change in deductible: - effect on EP

¹ Part (c) requires knowledge of methods for overall indications from Werner08.Indication - Chapter 8

² Part (a) contains an error in the examiner's report but their final answer is correct. The calculation should be: 750 + 900 + 1650 = 3300. (Both sample solutions wrote 1950 instead of 1650)

³ Click for a | forum thread explaining the examiner's report solution.

Full BattleQuiz You must be logged in or this will not work.

In Plain English!

Intro

Recall the Fundamental Insurance Equation:

premium = (Losses + LAE + U/W Expenses) + U/W profit

This is the insurance version of the basic formula price = cost + profit, where cost equals the term in parentheses. In this chapter, we focus on the premium portion of the equation. The goal in a pricing analysis is to determine whether current rates (premiums) are adequate to cover profit and costs, and to assess the need for future rate changes. The problem is that we cannot simply use raw premium data in our analysis. If we do, our conclusions may be wrong. Here are 3 specific items that can impact our premium data:

rate changes

→ to account for this, we will recalculate premiums at current rate level or CRL

changes in the mix of business, inflation

→ to account for this, we will trend the premium

development of premium (similar to development of losses)

→ this applies to incomplete PYs or lines of business using premium audits (not covered in detail in Werner)

Premium Aggregation

Premium aggregation works exactly the same way as exposure aggregation. After aggregating the exposures, all you then have to do is multiply by the given premium. There's a web-based practice problem in the next quiz as well as relevant old exam problems:

mini BattleQuiz 1 You must be logged in or this will not work.

Adjustments to Premium: Current Rate Level

Intro to Current Rate Level

Suppose we used data from 2022, 2023, and 2024 for a pricing analysis and our new rates are planned to go into effect on July 1, 2026. Our historical experience period is the 3 years 2022, 2023, 2024, and our effective date is July 1, 2026. Werner and Modlin have a perfect example that explains why adjusting raw premiums from the experience period to current rate level (CRL) is necessary.

EXAMPLE: Why is it necessary to adjust historical premium to CRL?

You can think of premiums at CRL as being the premiums you would have received from historical policies if they had been sold today with all the prior rate changes in effect. You might sometimes be asked to "on-level" the premiums. This means the same thing as bringing premiums to current rate level.

Pop Quiz A! :-o

If policies in your historical experience period were written at an average rate of $200 (as in the text example) but there was a subsequent rate change of -15%, what would the correct rate change for the future ratemaking time period have been? Assume the the "true" indicated rate for the future period is $220 (as in the text example). (thx CG!)

If you did not make the CRL adjustment, would your rate change be too high or too low? Click for Answer

Extension of Exposures

This is the most accurate method for bringing premiums to CRL but unfortunately it's the most difficult to implement. It involves recalculating the premium for every policy using the rates currently in effect. It requires that policy data is readily available and that system resources are sufficient to crunch that data. In the past this was simply not possible but increases in computing power are such that theoretically it could now be done. The issue is that legacy systems were not set up to accommodate this and significant resources would be required to re-engineer the processes involved.

The text provides a nice simple example. Suppose the rating algorithm to determine premium charged is:

Premium = Exposure x (Rate per Exposure) x (Class Factor) + Policy Fee.

Suppose that for this historical experience period we had the following:

Rate per Exposure = $900
Class Factor = 0.60
Policy Fee = $1,000

Then the premium for 1 exposure in this class of exposures = 1 x $900 x 0.60 + $1,000 = $1,540. Let's suppose that the company implemented changes to its rating variables as follows:

new Rate per Exposure = $1,045
new Class Factor = 0.70
new Policy Fee = $1,090

Then the premium @ CRL for this same exposure = 1 x $1,045 x 0.70 + $1,090 = $1,821.50. Now do the same thing for every policy in your book of business. Alice always wondered why this method is called extension of exposures. Why not just call it what it is: re-rating all policies?

Sometimes an exam problem will ask you to calculate the CRLF or Current Rate Level Factor. It's also called the OLF or On-Level Factor and for the above example, it's very easy:

CRLF = (EP @ CRL) / (original EP) = 1,821.50 / $1,540 = 1.183

This is what you're asked to do in part (b) of the following problem. Parts (a) is about the parallelogram method which we'll get to in the next section.

E (2018.Fall #3)

Parallelogram Method

We're going to cover the parallelogram method starting with a very simple example then build to more complicated examples.

Example A: Basic CRL Calculation

You and Alice are doing a pricing analysis for an insurer that began writing business on Jan 1, 2019, and you have selected CY 2020 and 2021 as your experience period.(Later on, we'll do similar calculations for Policy Year premium, but don't worry about that for now. The PY case is actually easier.) Anyway, let's say you're given the following CY earned premiums:

CY	EP
2020	100
2021	175

Ian the Intern also kindly looked up the rate change history and found there had been 1 rate change of 10% on Jan 1, 2021. So we have 2 sets of policies at 2 different rate levels. The first set of policies includes those with effective dates between Jan 1, 2020 and Dec 31, 2020; the second set includes those with effective dates on or after Jan 1, 2021. For our purposes we care only about relative rates, not actual rates, so we can arbitrarily set the relative rate level of the first set of policies equal to 1.0. The second set of policies then has a relative rate level of 1.0 x (1 + 10%) = 1.0 x 1.1 = 1.1. And since there was only 1 rate change, this is the current rate level or CRL. We'll need this value further down. (I told you we were going to start with an easy example. These numbers couldn't possibly be any simpler!)

So, as the first step in your pricing analysis, you'll need to find EP @ CRL. (Earned Premium at Current Rate Level). Here are the formulas and notation you'll need:

EP_CY = Earned Premium for calendar year CY (unadjusted premium data)

EP_CY @ CRL = Earned Premium for calendar year CY at Current Rate Level

CRLF_CY = Current Rate Level Factor for calendar year CY

The formula is as shown below but you don't yet have all the numbers:

EP_CY @ CRL = EP_CY x CRLF_CY

We were given EP_CY directly but you have to calculate CRLF_CY. Let:

CRL = Current Rate Level

ARL_CY = Average Rate Level for calendar year CY

Then we can use the following formula but we still don't quite have everything we need:

CRLF_CY = CRL / ARL_CY

We know CRL = 1.1 because we calculated it above as the product of all the prior rate changes. (Recall there was only 1 rate change). And for this example I'm just going to give you the ARL values.

ARL₂₀ = 1.00

ARL₂₁ = 1.05

The we can calculate the CRL factors using the formula from above:

CRLF₂₀ = 1.1 / 1.00 = 1.1

CRLF₂₁ = 1.1 / 1.05 = 1.0476

And finally we have what we need to solve the original problem of finding EP @ CRL:

EP₂₀@CRL = EP₂₀ x CRLF₂₀ = 100 x 1.1 = 110

EP₂₁@CRL = EP₂₁ x CRLF₂₁ = 175 x 1.0476 = 183.3

Example B: Calculating ARL (Average Rate Level)

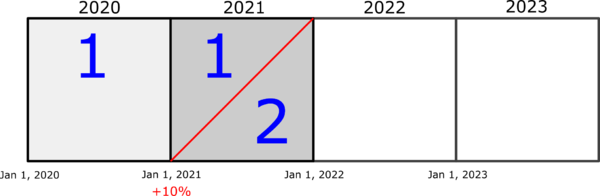
It might be an idea to do a 5-minute review of the Geometric Interpretation of exposure earnings because it's absolutely critical that you understand it. Premium earnings work exactly the same way. Here's the diagram corresponding to Example A but now we're going to fill in the missing detail and show how ARL (Average Rate Level) was calculated:

The rate change of +10% on Jan 1, 2021 is represented by the red diagonal line. This red line separates the policies into 2 rate groups and every policy within a rate group is charged the same rate:

Rate Group 1

consists of the whole CY 2020 square and the upper triangular portion of the CY 2021 square
the relative rate for this group is 1.0

Rate Group 2

consists of the lower triangular portion of the CY 2021 square
the relative rate for this group is 1.0 x (1 + 10%) = 1.10

The average rate level for CY 2020, ARL₂₀, is 1.0. This is trivial because every policy that has earnings in CY 2020 is at the 1.0 rate level. (Note that this includes policies written in 2019 with earnings in 2020.) To continue, we going to make an assumption:

Parallelogram Method Assumption: policies are written and earned uniformly across the experience period

Given this assumption, the average rate level for CY 2021, denoted by ARL₂₁, is an area-weighted average of the two rate levels in the CY 2021 square. If the sides of the square are each of length 1.0 then the area of the square is 1.0 so the upper and lower triangles each have an area of 0.5. We can now calculate the average rate level as follows:

ARL₂₁

= (upper area) x (rate level 1) + (lower area) x (rate level 2)

= 0.5 x 1.0 + 0.5 x 1.10

= 1.05

Note we don't care about CY 2022 or 2023 because that isn't part of our experience period. Anyway, Examples A and B together demonstrate the full parallelogram method.

This quiz has several CRL problems but for now just try the first problem. We'll cover how to do the others further down.

Alice's secret to learning the parallelogram method: This method can be confusing at first. it's best to first practice on the easy version which is annual policies with just 1 rate change. That's the first web-based problem in the quiz below and you should practice it until you consistently get the right answer. That's the most common type of calculation on the exam anyway. The other cases (6-month policies, policy year diagrams, and law changes) aren't tested as often and trying to absorb all of that at once might be too much. If you run into an exam problem where you need to do that, you can always refer back. Of course eventually you will need to learn all the different types of parallelogram problems, but you don't have to do it all at once. That's the secret. It just takes time for all of this new knowledge to sink in.

mini BattleQuiz 2a You must be logged in or this will not work.

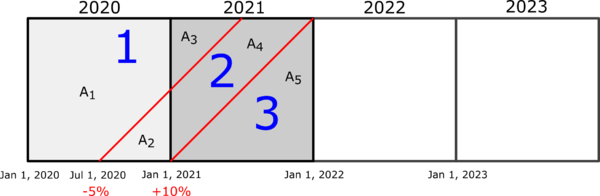
Example C: Two Rate Changes

Let's build on the previous examples by inserting another rate change. Conceptually it's the same but it's more fiddly because you have to calculate the areas of different polygons to get the average rate levels. We'll use the same premiums as in Examples A and B (100 and 175 for CY 2020 and 2021 respectively) but here's the new rate change information:

effective date of change	percentage rate change
Jul 1, 2020	-5%
Jan 1, 2021	+10%

Normally the exam problem will not provide the diagram so you'll have to learn how to draw it yourself. (You'll get practice in the upcoming quiz.) The red diagonals representing the rate changes separate the policies into 3 different rate level groups where policies within the same group are all charged the same rate.

You can see how these diagrams can quickly get cluttered and messy with all the different geometric areas. (When I'm drawing diagrams by hand I usually write in the rate levels for each group as well but I didn't want to clutter the picture.) The first thing to do is calculate CRL (Current Rate Level). This is easy because it's just the product of all the rate changes within the experience period based on an initial relative rate of 1.0:

CRL = 1.0 x (1 - 5%) x (1 + 10%) = 1.045

Now let's identify the portions of the diagram corresponding to the different rate groups and calculate the rate level for each:

Rate Group 1

consists of areas A₁, A₃
rate level = 1.0 ← this is the initial relative rate level

Rate Group 2

consists of areas A₂, A₄
rate level = 1.0 x (1 - 5%) = 1.0 x 0.95 = 0.95 ← this is the product of all prior rate changes

Rate Group 3

consists of area A₅
rate level = 1.0 x (1 - 5%) x (1 + 10%) = 1.0 x 0.95 x 1.10 = 1.045 ← this is the product of all prior rate changes and equal to CRL since there are no more rate changes

To get the ARL values (Average Rate Levels) for each CY, we basically need to calculate the areas of a bunch of different triangles within the picture. I delegated that task to Ian-the-Intern and here's what he came up with. Notice he had to do A₂ first but I listed them in 1-2 order to keep the presentation organized.

A₁ = 1.0 - A₂ = 7/8 = 0.875

A₂ = ½ x base x height = ½ x ½ x ½ = 1/8 = 0.125

Now we have what we need for ARL₂₀:

ARL₂₀ = A₁ x (rate level 1) + A₂ x (rate level 2) = (0.875 x 1.0) + (0.125 x 0.95) = 0.9938

I sent Ian back to his desk to calculate the other areas. Notice that he did A₃ and A₅ first. You better check his work!

A₃ = ½ x base x height = ½ x ½ x ½ = 1/8 = 0.125

A₄ = 1 - A₃ - A₅ = 1 - 0.125 - 0.5 = 0.375

A₅ = ½ x base x height = ½ x 1.0 x 1.0 = 1/8 = 0.5

Then:

ARL₂₁ = A₃ x (rate level 1) + A₄ x (rate level 2) + A₅ x (rate level 3) = (0.125 x 1.0) + (0.375 x 0.95) + (0.5 x 1.045) = 1.00375

Finally we have all the pieces and can now apply the formulas we learned in Example A:

CRLF_CY = CRL / ARL_CY

Substituting our numbers:

CRLF₂₀ = 1.045 / 0.9938 = 1.0515

CRLF₂₁ = 1.045 / 1.00375 = 1.0411

And the last formula we need is:

EP_CY @ CRL = EP_CY x CRLF_CY

So the final answer is:

EP₂₀ @ CRL = 100 x 1.0515 = 105.2

EP₂₁ @ CRL = 175 x 1.0411 = 182.2

Being able to calculate of EP at Current Rate Level is a foundational skill. Now you're ready to try the second problem in the quiz.

mini BattleQuiz 2b

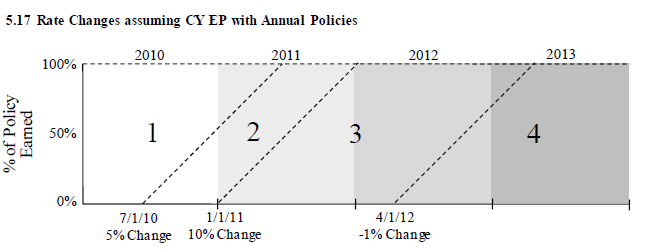
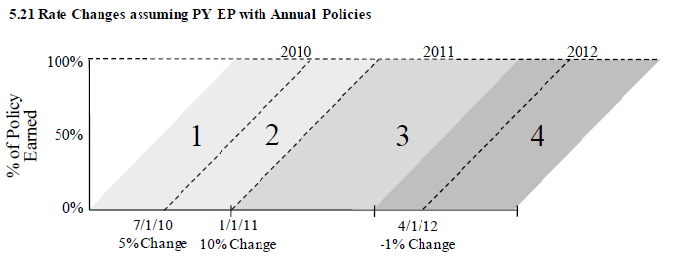
Example D: Werner (CY EP, Annual Policies)

I've pulled an example out of Werner as a Pop Quiz. Below is the diagram and you have to find CRLF₂₀₁₁, the Current Rate Level Factor for CY 2011. That's as far as you can go because you're aren't given any premiums. Note there are 3 rate changes and 4 CYs in the experience period so there would be a fair bit of work to find EP @CRL for all 4 years. Obviously this task should be done by the computer (or Ian-the-Intern.)

The answer is CRLF₂₀₁₁ = 1.0431. If you get stuck, click on the link to the solution in the source text...

SOLUTION: CRLF₂₀₁₁

Example E: Policies other than Annual

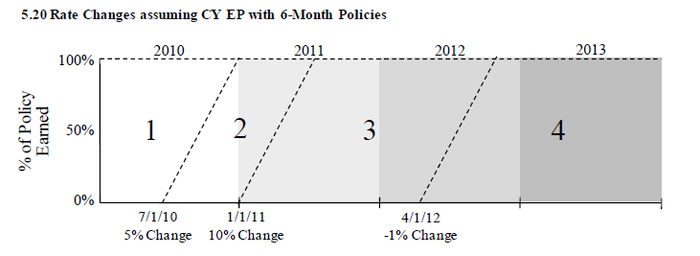
If you've practiced the first 2 web-based problems in quiz 1, then you'll have no trouble with extending the method to policies with terms that are either shorter or longer than 6 months. Here's the example of 6-month policies from the source text. The only difference is that the diagonal lines separating the rate changes have a slope of 2 instead of 1. See if you can find CRLF₂₀₁₁.

Check your answer in this link:

SOLUTION: CRLF₂₀₁₁ (6-month policies)

The third problem in the quiz deals with 6-month policies.

mini BattleQuiz 2c

And here's an old exam problem where part (c) has policies with 2-year terms. You should also try parts (a) and (b) but part (b) is hard. The basic parallelogram method assumes policies are written uniformly over the experience period but here that's not true. This changes how you calculate average rate levels because the average is no longer proportional to the geometric area.

E (2014.Spring #1)

Example F: Policy Years versus Calendar Years

There are a couple of more types of CRL problems but they are both pretty much the same as the ones we've already covered. The only difference is the shapes of the areas you have to calculate. Here we look at calculating EP @ CRL for policy years instead of calendar years although PYs doesn't show up nearly as often on the exam. It's easier than the CY case because there aren't any triangles. The rate changes lines have the same slope as the lines that separate the policy years so the shapes are all parallelograms and calculating the area of parallelograms is easy. If you've got 6-month policies instead of annual policies, the slopes of the lines are 2 instead of 1 but it's still easy because all the lines are still parallel. Here's the example from Werner. See if you can find CRLF_PY-2012.

Here's the link to the page in the source text with the answer.

SOLUTION: CRLF₂₀₁₂ (Policy Year)

The fourth problem in the quiz deals with PY premiums.

mini BattleQuiz 2d

Here's an old exam problem asking you to calculate EP @ CRL for policy years:

E (2017.Spring #2)

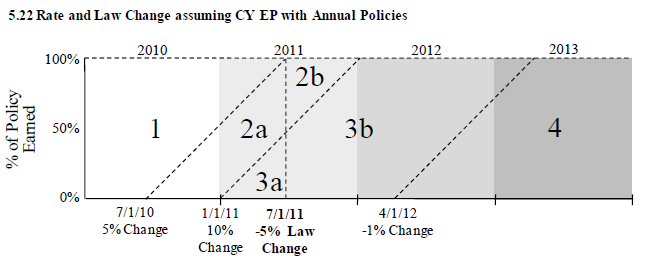
Example G: Law Change

This next example considers the case of a law change that affects the rate of all in-force policies. Compare this to the previous examples in which the rate change applied only to policies written on or after the date of the change. Geometrically, this law change is represented by a vertical line in the diagram. Rate level 2 and rate level 3 are each split into 2 groups so now the diagram has 5 different rate levels:

As in the previous examples from the source text, can you calculate CRLF_CY-2011 for the given rate changes. If you get stuck, here's the link to the solution from the text:

SOLUTION: CRLF₂₀₁₁ (with Law Change)

The fifth problem in the quiz deals with PY premiums.

mini BattleQuiz 2e

Example H: Uneven Distribution of Writings

The main assumption or drawback of the standard parallelogram method is that policies are written evenly over the year. If this is not the case, current rate level factors from the parallelogram method may not be accurate. The advantage of the extension of exposures method is that it doesn't make this assumption and will be accurate when policies are not written uniformly over time.

In simple cases however, the parallelogram method can be modified to take into account an uneven distribution. Here are 2 exam problems where you have to do that:

E (2015.Spring #5) ← part (b)

E (2014.Spring #1) ← part (b)

Adjustments to Premium: Trending

Intro to Premium Trending

Now is a good time to stop and think about where we are. You've just learned a bunch of different ways of calculating EP @ CRL but you don't yet know how that fits into the bigger picture. The current rate level calculation is just one piece of an overall rate level indication but we're not going to put all the pieces together until Chapter 8 - Indications. For now, just trust that if you follow along and do the practice problems that everything will eventually fall into place. The next piece of the indication "puzzle" is premium trending.

The reasons for trending premiums are similar to the reason for expressing EP @ CRL. Click here for a quick review of that. Premium levels can change over time but for a pricing analysis you need all the data to be "on the same level".

Question: identify causes for changes in premium level over time

inflation:

- can occur in lines of business with inflation-sensitive exposure bases like WC (payroll) or General Liability (sales receipts)

distributional shift due to:

- moving all insureds to a higher deductible (may cause a 1-time shift downward in premium)

- purchasing an entire portfolio of business from another insurer (may cause a 1-time shift upward or downward depending on how the characteristics of the current book compare to the new book)

Whatever the specific cause, we need a way to measure and then incorporate the premium trend into our analysis.

Question: how are premium trends typically measured

premium trends are typically measured using average written premium at current rate level: AWP @ CRL

Question: why do we use written premium to measure trends (instead of earned premium which is used in other parts of the pricing analysis)

written premium reflects shifts in distribution more quickly than earned premium (earned premium is spread over the policy term whereas written premium is immediate)

Question: why do we use changes in average premium to measure trends (instead of changes in total premium)

because if a company is growing or shrinking, total premium will change even if there is no distributional change in types of policies (may seem like there is a trend when there really isn't one)

Question: why do we use AWP at current rate levels instead of historical rate levels to measure the trend percentage

because rate changes over the experience period might look like a trend (they aren't unless the rate changes continue similarly) and this could lead to "double-counting" of the trend effect

Here's the example from Werner demonstrating a typical way of measuring premium trend. The final trend selection is judgmental and is based on column (5), Annual Change. In this case, 2% seems a reasonable final selection:

Here are a few important observations from this table:

the trend measurement and selection is based on column (4), average written premium @ CRL
column (5), the annual change column, compares like quarters

→ for 1Q10: 2.1% = (728.11 / 713.44) - 1

→ for 2Q10: 1.8% = (741.30 / 728.11) - 1

→ these are annual trends

The obvious final trend selection based on this data is 2.0%. Theoretically you could calculate changes between successive quarters or rows in the table, which would give you a quarterly trend. You could then calculate the 4th power to convert it to an annual trend and make your final trend selection based on that. A potential problem however is volatility in quarterly data.

The last thing I want to mention before getting into the actual calculations is in the difference between 1-step and 2-step trending. You can use 1-step trending if the premium trend is stable over time. This may be the case when inflation is the driving factor because inflation is generally continuous and stable. You should use 2-step trending however if historical premium trends are expected to be different from future trends. The text example of when 2-step trending may be appropriate is:

If the company had forced all insureds to a higher deductible at their first renewal on or after January 1, 2011, the shift would have been completed by December 31, 2011, and the observed trend will not continue into the future. When situations like this occur, companies may use a two-step trending approach.

mini BattleQuiz 3 You must be logged in or this will not work.

1-Step Trending

In the previous section we looked briefly at the text example for measuring and selecting a trend. The other piece to trending is the trend period and this can be tricky when you first learn it.

Question: what is the trend period for 1-step premium trending

it is the length of time between the following dates:

AWD (Average Written Date) of policies with premium earned during the historical experience period (this is tricky)
AWD of policies that will be in effect during the effective period (this is easy)

Ok, but how in the heck do you actually do the calculation?? The first one is tricky because you need the average written date for policies earned during a certain period. We'll look at an example then you can practice the calculation in the next quiz.

Suppose your historical period is CY 2011, which is Jan 1, 2011 to Jan 1, 2012. (Technically, the period ends Dec 31, 2011, but it's easier to follow the calculations if we use Jan 1, 2012. And it makes no difference to the final result.)
Suppose your planned rate change is Jan 1, 2013 and those rates will be in effect for 1 year, meaning the effective period is Jan 1, 2013 to Jan 1, 2014. (Technically the period ends Dec 30, 2013, but we're going to ignore that.)
Suppose also that we're considering only annual policies. (The policy term is important.)

(We also assume uniform writing over time unless specified otherwise)

We want AWD for the historical period and effective period:

AWD for policies earned in the historical period CY 2011 is: Jan 1 2011

Reasoning:

→ annual policies with earnings in CY 2011 could have been written anytime between Jan 1, 2010 and Jan 1, 2012 (this is the key observation)

→ the Average Written Date is just the midpoint of this 2-year writing period: Jan 1, 2011

AWD (Average Written Date) for policies written in the effective period Jan 1, 2013 to Jan 1, 2014 is midpoint of the period: July 1, 2013

The second one is easy because you're asked for the average written date for written policies. It matches up. Anyway, the trend period is then 2.5 years, the length of time between these 2 dates. The geometric interpretation is as shown in the example below from the source text. I actually don't find this type of diagram helpful here in the same way as for the current rate level calculations we did earlier but it doesn't hurt to include it.

Note that the historical period is a CY (Calendar Year) but the effective period is a PY (Policy Year).

As an aside, you can also calculate the trend period as the length of time between average earned dates. You get the same answer because the start and end average earned dates are shifted by the same amount relative to the start and end average written dates:

AED (Average Earned Date) for policies earned in the historical period CY 2011 is the midpoint of the period: July 1 2011

AED for policies written in the effective period Jan 1, 2013 to Jan 1, 2014 is: Jan 1, 2014

Reasoning:

→ annual policies with writings in this effective period will be earned between Jan 1, 2013 and Jan 1, 2015 (this is the key observation)

→ the Average Earned Date is just the midpoint of this 2-year earning period: Jan 1, 2014

The length of time between Jul 1, 2011 and Jan 1, 2014 is again 2.5 years. Let's now see how the trend period changes if we assume 6-month policies instead, but with the historical and effective periods as before.

Date calculations for 6-month policies:

First we'll do it with AWDs:

AWD for policies earned in the historical period CY 2011 is: Apr 1 2011

→ 6-month policies with earnings in CY 2011 could have been written anytime between July 1, 2010 and Jan 1, 2012 (this is the key observation - you go back only 6 months from the start of the historical period this time)

→ the Average Written Date is just the midpoint of this 1.5-year writing period: Apr 1 2011

AWD for policies written in the effective period Jan 1, 2013 to Jan 1, 2014 is midpoint of the period: July 1, 2013

The trend period is the length of time between these 2 dates which is 2.25 years. And for the sake of illustration let's do it with AEDs just to make sure you get the same answer.

AED for policies earned in the historical period CY 2011 is the midpoint of the period: July 1 2011

AED for policies written in the effective period Jan 1, 2013 to Jan 1, 2014 is: Oct 1, 2013

→ 6-month policies with writings in this effective period will be earned between Jan 1, 2013 and July 1, 2014 (this is the key observation - you go forward only 6 months from the end of the effective period this time)

→ the Average Earned Date is just the midpoint of this 1.5-year earning period: Oct 1, 2013

And again the trend period, or length of time between these 2 dates, is 2.25 years.

It's good to understand the reasoning behind calculating average written and earned dates for historical and effective periods but there are also formulas you can use:

AWD for policies earned during CY historical period = (mid-point of historical period) – 0.5 x (policy term) AWD for policies written during PY effective period = (mid-point of effective period)

There are similar formulas for the AED dates:

AED for policies earned during CY historical period = (mid-point of historical period) AED for policies written during PY effective period = (mid-point of effective period) + 0.5 x (policy term)

And remember, the trend periods are the same regardless of whether you use written or earned dates. For trending we normally we think in terms of AWDs however since the measurement and selection of premium trends is usually based on average written premium.

Part (a) of this old exam problem uses 1-step trending. The way they calculate the trend percentage using AWP (Average Written Premium) is slightly different from the way it was presented in Werner. Also, it might help to first do the web-based practice problem on 1-step trending. See below.

E (2013.Spring #2)

The first problem in the quiz is a web-based problem for practice in calculating the trend period for 1-step trending.

mini BattleQuiz 4a

2-Step Trending

Recall that 2-step trending is more appropriate than 1-step trending if historical trends and future trends are expected to be different. With 2-step trending, we split the trend period into 2 pieces so we can apply a different trend percentage to each piece.

Question: what are the 2 trend periods in 2-step premium trending

period 1 start

→ AWD for policies earned during the historical period (same start as for 1-step trending)

period 1 end

→ mid-point of latest period available in the data

period 2 start

→ mid-point of latest period available in the data (same as period 1 end)

period 2 end

→ AWD for policies written during effective period (same end as for 1-step trending)

Basically, we added an intermediate point to the original 1-step trend: the mid-point of the latest period available in the data.

Let's go back to the example from Werner to see how 2-step trending works. We want to trend CY 2011, and the latest available data point is 4Q11.

The period 1 trend starts at the AWD of policies earned during CY 2011, which is Jan 1, 2011. The period 1 trend ends at the midpoint of the latest available data point, which is Nov 15, 2011. The length of the period 1 trend is 10.5/12 = 0.875 years. (The step 1 trend period is different depending on the CY being trending. For example the step 1 trend period for CY 2010 would be 1.875.)

So far, so good. But what value do we use for the trend percentage. You could use a selected trend of 2% from the above table but often in 2-step trending, we use the following "trend factor" or "adjustment factor" instead: (This factor is then applied to the historical EP)

step 1 adjustment factor = (latest AWP @ CRL) / (historical AEP @ CRL) ← different for each CY in historical period

We can read the numerator directly from the table: 753.00. The denominator was not given but the text simply tells you to assume that AEP @ CRL = 740.00 (Average Earned Premium @ Current Rate Level.) Then the adjustment factor is 753/740 = 1.0176. This value will be inserted into the summary table further down.

Now let's do step 2:

step 2 trend factor = (1 + selected future trend)^{(step 2 trend period)} ← same for each CY in historical period

The period 2 starts where the period 1 trend ended: Nov 15, 2011. The period 2 trend ends at the AWD for policies written during the effective period. The effective period was given as Jan 1, 2013 to Jan 1, 2014 so the AWD is July 1, 2013. The length of the period 1 trend is (1.5 + 12 + 6) / 12 = 1.625 years. (The step 2 trend period is the same for every CY being trended.)

Based on data not provided, a future trend of -1% was selected. (The historical trend seems to be 2% judging from the data table.) Anyway, the step 2 trend factor is (1 - 1%)^1.625 = 0.9838. The text then summarizes the calculation in a table:

Werner05 (120) summary 2 step trending.png

Pop Quiz B! :-o

Where was the step 1 trend period of 0.875 used? Click for Answer

Here's a link to a good exam problem using 2-step trending. You can do it with what we've covered so far but notice the examiner's report provided 5 different sample answers. Sample answer #1 is probably the best because it follows the exact method outlined above. The other sample answers are slight variations but are definitely worth looking at.

E (2017.Fall #1)

Before getting to the quiz for practice in 2-step trending, there's one last thing to mention. I hate to add this to an already long chapter but it's discussed briefly in the text so you should at least be aware of it even it if isn't likely to be asked on the exam. It's an alternate way to do step 1 as part of 2-step trending. Instead of using the ratio of AWP to AEP as stated above, you could select a historical trend percentage and trend each CY in the historical period in the "normal" way. It's here that you would explicitly use the step 1 trend period. (Recall that previously the step 1 trend period was not actually used.) The end of each step 1 period is the same, the mid-point of the latest available data period, but the start of each period depends on the CY as described above. If you've practiced the web-based problem in calculating the trend period for 1-step trending then you'll be able to do this.

alternate step 1 adjustment factor = (1 + selected historical trend)^{(step 1 trend period)} ← different for each CY in historical period

If the selected historical trend is 2% then the step 1 adjustment factor (or step 1 trend factor) for CY 2011 would be 1.02^0.875.
Similarly, the trend factors for CY 2010 and CY 2009 would be 1.02^1.875 and 1.02^2.875 respectively.

The second problem in the quiz provides more practice for 2-step trending.

mini BattleQuiz 4b

Adjustments to Premium: Development

Premium development is the third way premium data may need to be adjusted before being used in a rate analysis. Werner has a very nice description of the concept of premium development:

In some cases, the actuary may not know the ultimate amount of premium for the experience period at the time the analysis is being performed. When this occurs, the actuary must estimate how the premium will develop to ultimate. Common scenarios include when an actuary is using an incomplete year of data or when the line of business uses premium audits.

See part (d) of this exam problem for a very easy concept problem on premium development:

E (2017.Spring #2)

Here's a simple numerical example from Werner of how to calculate a premium development factor. (There is a link to 2 further practice problems below the examples.)

Here are 2 practice problems similar to the example:

Practice: 2 premium development problems (like Werner example)

POP QUIZ ANSWERS

Yes, for a calendar year. No for a policy year.

→ If an insurer has 1 annual policy written on July 1, 2024 but cancelled on Apr 1, 2025, then CY 2025 will have a negative written exposure of-0.25. (The written exposure for CY 2024 would be 1.00 so the total across 2 years would be 0.75.)

→ This cannot happen for a policy year because the effect of a cancellation would be recorded in the same policy year the exposure was written.

Go back

Pop Quiz A - Answer

First, adjust the historical average premium of $200 to CRL (Current Rate Level):

→ $200 x (1 - 15%) = $170

Second, calculate the rate change required to bring $170 up to $220:

→ $220 / $170 - 1 = 29.4%

If you did not make the CRL adjustment you would have calculated a rate change of $220 / $200 - 1 = 10%, which would have been too low.

Go back

Pop Quiz B - Answer

The step 1 trend period of 0.875 was not used. The first adjustment in this version of 2-step trending is just the ratio of (AWP for the latest quarter) to (AEP for the historical period). The length of the trend period is not relevant. There is a version of 2-step trending that does use the step 1 trend period and we'll cover it briefly but it isn't used as often.

Go back