Werner05.Premium

Reading: BASIC RATEMAKING, Fifth Edition, May 2016, Geoff Werner, FCAS, MAAA & Claudine Modlin, FCAS, MAAA Willis Towers Watson

Chapter 5: Premium

BattleTable

Based on past exams, the main things you need to know (in rough order of importance) are:

• parallelogram method - calculating current rate level factors (on-level factors), advantages / disadvantages
• fact B...

reference	part (a)	part (b)	part (c)	part (d)
E (2019.Fall #2)	CYWP: - calculate	in-force premium: - calculate	CYWP: - calculate	(d) EP estimate using IFE (e) uses of IFE
E (2019.Spring #2)	premium trend, CRL - calculate	premium trend, CRL - effect of policy term
E (2018.Fall #2)	CYEP - calculate	PYLR - calculate
E (2018.Fall #3)	parallelogram method - on-level factor	extension of exposures - on-level factor	parallelogram method - appropriate?
E (2017.Fall #1)	premium trend: - 2-step trending	negative premium trend: - give examples
E (2017.Fall #2)	parallelogram method - EP @ CRL	rate change: - xxx method
E (2017.Fall #3)	CYEP, CYWP - calculate	PYEP, PYWP - calculate	CY aggregation: - ads & disads
E (2017.Spring #2)	parallelogram method - EP @ CRL (PYs)	Werner07.OtherExpenses	parallelogram method - appropriate?	PY premium - change after PY end
E (2016.Fall #2)	parallelogram method - on-level premiums	parallelogram method - weaknesses
E (2016.Spring #2)	CYWP: - calculate	CYEP: - calculate	in-force premium: - calculate	CYEE: - by territory
E (2015.Fall #1)	CYWE, CYEE: - calculate	parallelogram method - on-level premiums	extension of exposures - on-level premiums
E (2015.Spring #4)	parallelogram method - on-level premiums	premium trend - select & apply trend
E (2015.Spring #5)	parallelogram method - on-level premiums	parallelogram method - with uneven writings	alternate on-level method - suggest a method
E (2014.Fall #2)	CYEP: - calculate	CYWP: - calculate	PYEP: - calculate	PYWP: - calculate
E (2014.Fall #3)	parallelogram method - pros / cons	extension of exposures - pros / cons
E (2014.Spring #1)	parallelogram method - on-level factor	parallelogram method - uneven exposures	parallelogram method - 2-year policies
E (2013.Fall #2)	extension of exposures - on-level factor
E (2013.Spring #2)	premium trend: - 1-step trending	premium trend: - purpose	premium trend: - possible issues	change in deductible: - effect on EP

In Plain English!

Intro

Recall the Fundamental Insurance Equation:

premium    =    (Losses   +   LAE   +   U/W Expenses)   +   U/W profit

This is the insurance version of the basic formula price = cost + profit, where cost equals the term in parentheses. In this chapter, we focus on the premium portion of the equation. The goal in a pricing analysis is to determine whether current rates (premiums) are adequate to cover profit and costs, and to assess the need for future rate changes. The problem is that we cannot simply use raw premium data in our analysis. If we do, our conclusions may be wrong. Here are 3 specific items that can impact our premium data:

• rate changes

→ to account for this, we will recalculate premiums at current rate level or CRL

• changes in the mix of business, inflation

→ to account for this, we will trend the premium

• development of premium (similar to development of losses)

→ this applies to incomplete PYs or lines of business using premium audits and not covered in detail in Werner

Adjustments to Premium: Current Rate Level

Intro

Suppose we used data from 2022, 2023, and 2024 for a pricing analysis and our new rates are planned to go into effect on July 1, 2026. Our historical experience period is the 3 years 2022, 2023, 2024, and our effective date is July 1, 2026. Werner and Modlin have a perfect example that explains why adjusting raw premiums from the experience period to current rate level (CRL) is necessary.

EXAMPLE:   Why is it necessary to adjust historical premium to CRL?

You can think of premiums at CRL as being the premiums you would have received from historical policies if they had been sold today with all the prior rate changes in effect. You might sometimes be asked to "on-level" the premiums. This means the same thing as bringing premiums to current rate level.

Pop Quiz A!    :-o

• If policies in your historical experience period were written at an average rate of $200 (as in the text example) but there was a subsequent rate change of -10%, what would the correct rate change for the future ratemaking time period have been? Assume the the "true" indicated rate for the future period is $220 (as in the text example).

• If you did not make the CRL adjustment, would your rate change be too high or too low? Click for Answer 

Extension of Exposures

This is the most accurate method for bringing premiums to CRL but unfortunately it's the most difficult to implement. It involves recalculating the premium for every policy using the rates currently in effect. It requires that policy data is readily available and that system resources are sufficient to crunch that data. In the past this was simply not possible but increases in computing power are such that theoretically it could now be done. The issue is that legacy systems were not set up to accommodate this and significant resources would be required to re-engineer the processes involved.

The text provides a nice simple example. Suppose the rating algorithm to determine premium charged is:

Premium   =   Exposure   x   (Rate per Exposure)   x   (Class Factor)   +   Policy Fee.

Suppose that for this historical experience period we had the following:

• Rate per Exposure = $900
• Class Factor = 0.60
• Policy Fee = $1,000

Then the premium for 1 exposure in this class of exposures = 1 x $900 x 0.60 + $1,000 = $1,540. Let's suppose that the company implemented changes to its rating variables as follows:

• new Rate per Exposure = $1,045
• new Class Factor = 0.70
• new Policy Fee = $1,090

Then the premium @ CRL for this same exposure = 1 x $1,045 x 0.70 + $1,090 = $1,821.50. Now do the same thing for every policy in your book of business. Alice always wondered why this method is called extension of exposures. Why not just call it what it is: re-rating all policies?

Parallelogram Method

We're going to cover the parallelogram method by starting with a very simple example then build on that.

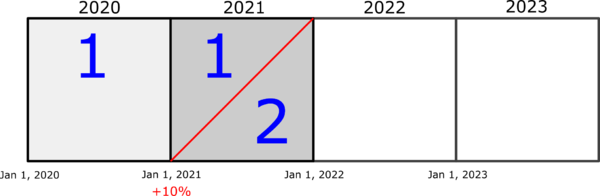
Example A: Basic CRL Calculation

You and Alice are doing a pricing analysis for an insurer that began writing business on Jan 1, 2019, and you have selected CY 2020 and 2021 as your experience period.(Later on, we'll do similar calculations for Policy Year premium, but don't worry about that for now. The PY case is actually easier.) Anyway, let's say you're given the following CY earned premiums:

CY	EP
2020	100
2021	175

Ian the Intern also kindly looked up the rate change history and found there had been 1 rate change of 10% on Jan 1, 2021. So we have 2 sets of policies at 2 different rate levels. The first set of policies includes those with effective dates between Jan 1, 2020 and Dec 31, 2020; the second set includes those with effective dates on or after Jan 1, 2021. For our purposes we care only about relative rates, not actual rates, so we can arbitrarily set the relative rate level of the first set of policies equal to 1.0. The second set of policies then has a relative rate level of 1.0 x (1 + 10%) = 1.0 x 1.1 = 1.1. And since there was only 1 rate change, this is the current rate level or CRL. We'll need this value further down. (I told you we were going to start with an easy example. These numbers couldn't possibly be any simpler!)

So, as the first step in your pricing analysis, you'll need to find EP @ CRL. (Earned Premium at Current Rate Level). Here are the formulas and notation you'll need:

EP_CY = Earned Premium for calendar year CY (unadjusted premium data)

EP_CY @ CRL = Earned Premium for calendar year CY at Current Rate Level

CRLF_CY = Current Rate Level Factor for calendar year CY

The formula is as shown below but you don't yet have all the numbers:

EPCY @ CRL   =   EPCY   x   CRLFCY

We were given EP_CY directly but you have to calculate CRLF_CY. Let:

CRL = Current Rate Level

ARL_CY = Average Rate Level for calendar year CY

Then we can use the following formula but we still don't quite have everything we need:

CRLFCY   =   CRL   /   ARLCY

We know CRL = 1.1 because we calculated it above as the product of all the prior rate changes. (Recall there was only 1 rate change). And for this example I'm just going to give you the ARL values.

ARL₂₀ = 1.00

ARL₂₁ = 1.05

The we can calculate the CRL factors using the formula from above:

CRLF₂₀ = 1.1 / 1.00 = 1.1

CRLF₂₁ = 1.1 / 1.05 = 1.0476

And finally we have what we need to solve the original problem of finding EP @ CRL:

EP₂₀@CRL = EP₂₀ x CRLF₂₀ = 100 x 1.1 = 110

EP₂₁@CRL = EP₂₀ x CRLF₂₀ = 175 x 1.0476 = 183.3

Example B: Calculating ARL (Average Rate Level)

It might be an idea to do a 5-minute review of the Geometric Interpretation of exposure earnings because it's absolutely critical that you understand it. Premium earnings work exactly the same way. Here's the diagram corresponding to Example A but now we're going to show how to calculate ARL (Average Rate Level) calculation works.

The rate change of +10% on Jan 1, 2021 is represented by the red diagonal line. This red line separates the policies into 2 rate groups and every policy within a rate group is charged the same rate:

Rate Group 1

• consists of the whole CY 2020 square and the upper triangular portion of the CY 2021 square
• the relative rate for this group is 1.0

Rate Group 2

• consists of the lower triangular portion of the CY 2021 square
• the relative rate for this group is 1.0 x (1 + 10%) = 1.10

The average rate level for CY 2020, ARL₂₀, is 1.0. This is trivial because every policy that has earnings in CY 2020 is at the 1.0 rate level. (Note that this includes policies written in 2019 with earnings in 2020.) To continue, we going to make an assumption:

Parallelogram Method Assumption: policies are written and earned uniformly across the experience period

Given this assumption, the average rate level for CY 2021, denoted by ARL₂₁, is an area-weighted average of the two rate levels in the CY 2021 square. If the sides of the square are each of length 1.0 then the area of the square is 1.0 so the upper and lower triangles each have an area of 0.5. We can now calculate the average rate level as follows:

ARL₂₁

=   (upper area) x (rate level 1)   +   (lower area) x (rate level 2)

=   0.5 x 1.0   +   0.5 x 1.10

=   1.05

Note we don't care about CY 2022 or 2023 because that isn't part of our experience period. Anyway, Examples A and B together demonstrate the full parallelogram method.

This quiz has several CRL problems but for now just try the first problem. We'll cover how to do the others further down.

mini BattleQuiz 1a You must be logged in or this will not work.

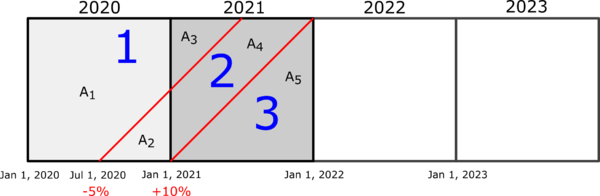
Example C: Two Rate Changes

Let's build on the previous examples by inserting another rate change. Conceptually it's the same but it's more fiddly because you have to calculate the areas of different polygons to get the average rate levels. We'll use the same premiums as in Examples A and B (100 and 175 for CY 2020 and 2021 respectively) but here's the new rate change information:

effective date of change	percentage rate change
Jul 1, 2020	-5%
Jan 1, 2021	+10%

Normally the exam problem will not provide the diagram so you'll have to learn how to draw it yourself. (You'll get practice in the upcoming quiz.) The red diagonals representing the rate changes separate the policies into 3 different rate level groups where policies within the same group are all charged the same rate.

You can see how these diagrams can quickly get cluttered and messy with all the different geometric areas. (When I'm drawing diagrams by hand I usually write in the average rate levels as well but I didn't want to clutter the picture.) The first thing to do is calculate CRL (Current Rate Level). This is easy because it's just the product of all the rate changes within the experience period based on an initial relative rate of 1.0:

CRL = 1.0 x (1 - 5%) x (1 + 10%) = 1.045

Now let's identify the portions of the diagram corresponding to the different rate groups and calculate the rate level for each:

Rate Group 1

• consists of areas A₁, A₃
• rate level = 1.0

Rate Group 2

• consists of areas A₂, A₄
• rate level = 1.0 x (1 - 5%) = 1.0 x 0.95 = 0.95

Rate Group 3

• consists of area A₅
• rate level = 1.0 x (1 - 5%) x (1 + 10%) = 1.0 x 0.95 x 1.10 = 1.045

To get the ARL values (Average Rate Levels) for each CY, we basically need to calculate the areas of a bunch of different triangles within the picture. I delegated that task to Ian-the-Intern and here's what he came up with. Notice he had to do A₂ first but I listed them in 1-2 order to keep the presentation organized.

A₁   =   1.0 - A₁   =   7/8   =   0.875

A₂   =   ½ x base x height   =   ½ x ½ x ½   =   1/8   =   0.125

Now we have what we need for ARL₂₀:

ARL₂₀   =   A₁ x (rate level 1)   +   A₂ x (rate level 2)   =   (0.875 x 1.0) + (0.125 x 0.95)   =   0.9938

I sent Ian back to his desk to calculate the other areas. Notice that he did A₃ and A₅ first. You better check his work!

A₃   =   ½ x base x height   =   ½ x ½ x ½   =   1/8   =   0.125

A₄   =   1 - A₃ - A₅   =   1 - 0.125 - .05   =   0.375

A₅   =   ½ x base x height   =   ½ x 1.0 x 1.0   =   1/8   =   0.5

Then:

ARL₂₁   =   A₃ x (rate level 1)   +   A₄ x (rate level 2)   +   A₅ x (rate level 3)   =   (0.125 x 1.0) + (0.375 x 0.95) + (0.5 x 1.045)   =   1.00375

Finally we have all the pieces and can now apply the formulas we learned in Example A:

CRLF_CY   =   CRL   /   ARL_CY

Substituting our numbers:

CRLF₂₀   =   1.045 / 0.9938   =   1.0515

CRLF₂₁   =   1.045 / 1.00375   =   1.0411

And the last formula we need is:

EP_CY @ CRL   =   EP_CY   x   CRLF_CY

So the final answer is:

EP₂₀ @ CRL   =   100 x 1.0515   =   105.2

EP₂₁ @ CRL   =   175 x 1.0411   =   182.2

Being able to calculate of EP at Current Rate Level is a foundational skill. Now you're ready to try the second problem in the quiz.

mini BattleQuiz 1b You must be logged in or this will not work.

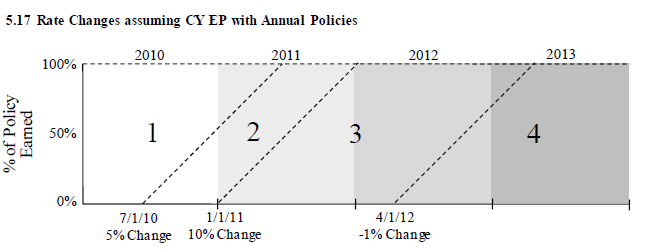
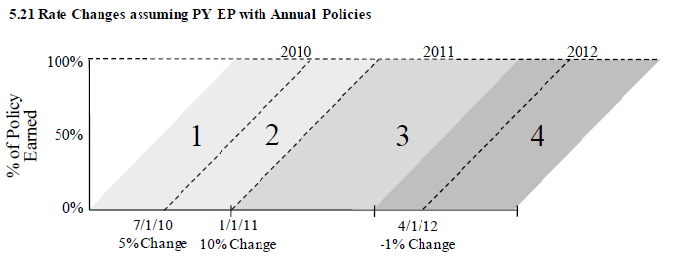
Example D: Werner (CY EP, Annual Policies)

I've pulled an example out of Werner as a Pop Quiz. Below is the diagram and you have to find CRLF₂₀₁₁, the Current Rate Level Factor for CY 2011. That's as far as you can go because you're aren't given any premiums. Note there are 3 rate changes and 4 CYs in the experience period so there would be a fair bit of work to find EP @CRL for all 4 years. Obviously this task should be done by the computer (or Ian-the-Intern.)

The answer is CRLF₂₀₁₁ = 1.0431. If you get stuck, click on the link to the solution in the source text...

SOLUTION:   CRLF₂₀₁₁

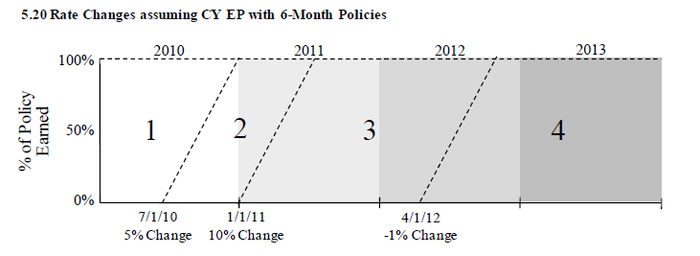
Example E: Policies other than Annual

If you've practiced the first 2 web-based problems in quiz 1, then you'll have no trouble with extending the method to policies with terms that are either shorter or longer than 6 months. Here's the example of 6-month policies from the source text. The only difference is that the diagonal lines separating the rate changes have a slope of 2 instead of 1. See if you can find CRLF₂₀₁₁.

Check your answer in this link:

SOLUTION:   CRLF₂₀₁₁ (6-month policies)

The third problem in the quiz deals with 6-month policies.

mini BattleQuiz 1c

And here's an old exam problem where part (c) has policies with 2-year terms. You should also try parts (a) and (b) but part (b) is hard. The basic parallelogram method assumes policies are written uniformly over the experience period but here that's not true. This changes how you calculate average rate levels because the average is no longer proportional to the geometric area.

E (2014.Spring #1)

Example F: Policy Years versus Calendar Years

There are a couple of more types of CRL problems but they are both pretty much the same as the ones we've already covered. The only difference is the shapes of the areas you have to calculate. Here we look at calculating EP @ CRL for policy years instead of calendar years although PYs doesn't show up nearly as often on the exam. It's easier than the CY case because there aren't any triangles. The rate changes lines have the same slope as the lines that separate the policy years so the shapes are all parallelograms and calculating the area of parallelograms is easy. If you've 6-month policies instead of annual policies, the slopes of the lines are 2 instead of 1 but it's still easy because all the lines are still parallel. Here's the example from Werner. See if you can find CRLF_PY-2011.

Here's the link to the page in the source text with the answer.

SOLUTION:   CRLF₂₀₁₁ (Policy Year)

The fourth problem in the quiz deals with PY premiums.

mini BattleQuiz 1d

Here's an old exam problem asking you to calculate EP @ CRL for policy years:

E (2017.Spring #2)

Pop Quiz A - Answer

• First, adjust the historical average premium of $200 to CRL (Current Rate Level):

→ $200 x (1 - 15%) = $170

• Second, calculate the rate change required to bring $180 up to $220:

→ $220 / $170 - 1 = 29.4%

• If you did not make the CRL adjustment you would have calculated a rate change of $220 / $200 - 1 = 10%, which would have been too low.

• Go back