Werner11.SpecialClass

Reading: BASIC RATEMAKING, Fifth Edition, May 2016, Geoff Werner, FCAS, MAAA & Claudine Modlin, FCAS, MAAA Willis Towers Watson

Chapter 11: Special Classification

Pop Quiz

Identify a data mining technique with the same name as the 4th planet of our solar system. Click for Answer 

Study Tips

VIDEO: W-11 (001) Special Classification → 7:15 Forum

This is a long chapter because it covers several different topics. I've indicated below which topics are the most frequently asked. You can also see this from the BattleTable.

• territorial analysis
• Increased Limits Factors (ILFs) ← frequently asked
• deductibles (pretty easy, you can usually figure it out just knowing the basic formulas)
• size of loss: premium discount, loss constant
• Insurance-to-Value (ITV) ← frequently asked

The first section on territorial analysis is the shortest and doesn't have any calculation problems. The other 4 topics in the list are heavy on calculations and there are roughly 8 web-based problems to help you learn the various methods. I've organized the quizzes so that most of the exam problems are at the end in quizzes 6,7, and 8. Do the web-based problems first. The exam problems are about the same level of difficulty but they usually also ask you to interpret the results.

The section on Increased Limits Factors contains a very difficult type of problem. Click here if you want to take a peek. Make sure to allocate time to learn and practice it.

Other than that, it's practice, practice, practice. And once you learn the different methods, put them aside and give yourself time to "forget". When you come back to them a few days later or a week or two later, you'll probably have trouble with them. That's expected. The act of trying to remember how to do them will reinforce them in your memory. When you learn them the second time, they will stick better than they did the first time. (And when you learn them the third time, you'll know them better than the second time, and so on. You might have to come back to them 5 or 6 times or more to be fully confident on exam day.)

Alice's Pro-Tip: Whenever you bring up a BattleCard quiz, the lapse column tells you how many days it has been since you last attempted that problem. Alice is always trying to make it easy for you to keep track of what you're doing!

Estimated study time: 1 week (not including subsequent review time)

BattleTable

Based on past exams, the main things you need to know (in rough order of importance) are:

• increased limits factors
• indemnity & coinsurance - this is the material on ITV or Insurance-to-Value

reference	part (a)	part (b)	part (c)	part (d)
E (2019.Fall #13)	increased limits factors - calculate
E (2019.Fall #14)	indemnity & coinsurance - calculate	indemnity & coinsurance - equitable rates	indemnity & coinsurance - adequate rates
E (2018.Fall #10)	territory classes - disadvantages	territory classes - creation of
E (2018.Fall #13)	rate for AOI levels -calculate	underinsurance - problems with	indemnity & coinsurance - calculate
(2018.Spring #14)	BA PowerPack Station 1
E (2017.Fall #12)	loss layers - compare expected losses	increased limits factors - are they appropriate?	increased limits factors - calculation method
E (2017.Fall #14)	indemnity & coinsurance - coinsurance percentage	indemnity & coinsurance - ITV initiatives
E (2017.Spring #11)	rate for AOI levels -calculate	underinsurance - problems with	indemnity & coinsurance - calculate
E (2016.Fall #11)	increased limits factors - calculate	loss layer - severity trend	increased limits factors - comment on method
E (2016.Fall #14)	indemnity & coinsurance - coinsurance penalty	indemnity & coinsurance - max coinsurance penalty	indemnity & coinsurance - coinsurance ratio	underinsurance - problems with
E (2016.Spring #9)	large deductible policy - calculate premium
E (2016.Spring #11)	increased limits factors - calculate	increased limits factors - impact of trend	loss layer - complement of credibility
E (2015.Spring #14)	increased limits factors - calculate	deductibles & limits - loss elimination ratio	deductibles & limits - pricing issues
E (2013.Fall #11)	increased limits factors - 2-dimensional data grid	increased limits factors - std method vs. GLM	increased limits factors - select & justify
E (2013.Fall #13)	SCENARIO - premium adequacy

Full BattleQuiz You must be logged in or this will not work.

In Plain English!

Territorial Ratemaking

Geography is a primary driver of claims experience and territory is a very commonly used rating variables. An insurer creates territories by grouping smaller geographic units such as zip codes or counties. An actuarial analysis then produces a relativity for each territory. The 2 steps in territorial ratemaking are:

[1] establishing boundaries

[2] determining relativities

Question: identify challenges to territorial ratemaking

• territory may be correlated with other rating variables

(Ex: AOI and territory are correlated because high-value homes are often clustered)

• territories are often small so data may not be credible

Keep these challenges in the back of your mind while we look a little more closely at the details involved in establishing territorial boundaries.

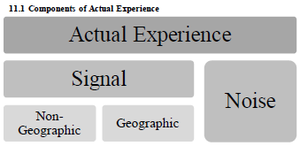
Step 1a in establishing territorial boundaries would be selecting a geographic unit, whether that's zip code or county or something else. Note that zip codes are easy to obtain but subject to change over time. Counties don't change but may be too large to be homogenous because they often contain both urban and rural areas. Werner and Modlin have a neat little diagram showing the components of actuarial experience.

What this diagram says is that the data, as we already know, consists of signal and noise. (Hopefully more signal than noise) The signal can come from many different sources but we want to isolate the geographic signal. The non-geographic signal would be due to variables like age of home or marital status and would be dealt with separately.

Step 1b in establishing territorial boundaries would be assessing the geographic risk of each unit using internal data and also possibly external data like population density or rainfall. The geographic risk is expressed by a geographic estimator, which for a univariate method could be pure premium, but univariate methods don't work well here. They don't account for correlations with other rating variables and may give volatile results on data sets with low credibility such as individual zip codes. Multivariate methods are the better option because they are able to account for exposure correlation. They also perform better at separating signal from noise on data sets with low credibility.

Step 1c involves addressing credibility issues using a technique called spatial smoothing. If a particular zip code doesn't have sufficient credible data, we can supplement it by "borrowing" data from a similar nearby zip code. The goal is to get a more accurate geographic estimator for the original zip code or geographic unit by supplementing our analysis with similar data. There are 2 spatial smoothing methods:

• distance-based - weight the given geographical unit with units that are less than a specified distance away from the given unit

→ closer areas get more weight

→ works well for weather-related perils

• adjacency-based - weight the given geographical unit with units that are adjacent to the given unit

→ immediately adjacent areas get more weight

→ works well for urban/rural divisions and for natural boundaries like rivers or artificial boundaries like high-speed rail corridors

Step 1d is the final step and involves clustering the individual units in to territories that are:

• homogeneous
• credible
• statistically significant (different territories have statistically significant differences in risk and loss experience)

See Reserving Chapter 3 - Homogeneity & Credibility for a quick review. There are a couple of different methods for clustering:

• quantile methods - create clusters with an equal number of observations (Ex: geographic units) or equal weights (Ex: exposures)
• similarity methods - create clusters based on similarity of geographic estimators

These clustering methods don't necessarily produce contiguous territories. There could be zip codes in opposite corners of a state that have the same geographic estimator and grouped into the same territory even if they are hundreds of kilometers apart.

Question: identify a drawback of creating too few territories

• fewer territories means larger jumps in risk at boundaries (and potentially large jumps in rate)

Question: identify a drawback of creating too many territories

• more territories means each is smaller and therefore less credible (although with increasing sophistication of methods, some insurers are moving towards smaller territories)

The text doesn't go into any further mathematical details of creating territories. It is beyond the scope of the syllabus of this. Alice thinks you should be ready to give this exam problem a try:

E (2018.Fall #10)

The quiz is easy...just a few things to memorize...

mini BattleQuiz 1

Increased Limits Ratemaking

Intro to Increased Limits

According to Werner

Insurance products that provide protection against third-party liability claims usually offer the insured different amounts of insurance coverage, referred to as limits of insurance. Typically, the lowest level of insurance offered is referred to as the basic limit, and higher limits are referred to as increased limits.

In Pricing - Chapter 9 we learned how to calculate relativities for different levels of rating variables. Here we do the same thing for the rating variable policy limit but the method is more complicated.

Example A: Individual Uncensored Claims

Alice-the-Actuary's company offers auto insurance at 2 different policy limits: 50k and 100k. These are single limits. Let's call 50k the basic limit because that's the minimum limit that's offered. We assign this basic limit a relativity of 1.0. Then 100k is an increased limit and we want to calculate its relativity against the basic limit. Let's make up some simple data so we can see how this works.

Suppose you've got 2 customers with a basic limits policy and they've submitted claims as follows:

• claim #1: $2,000
• claim #2: $4,000

Then the average severity is obviously $3,000. Easy. But what if claim #2 were instead $60,000? Since the policy limit is 50k, this claim must be capped at $50,000 and the average severity is ($2,000 + $50,000)/2 = $26,000. Still easy, but this is why increased limits ratemaking is more complicated than what we covered in Pricing - Chapter 9. Sometimes the company database keeps the value of the original $60,000 claim even though only $50,000 would be paid out, but sometimes this extra information is lost. The data processing system might cap the claim at $50,000 before entry and the fact that it was originally a $60,000 claim is lost forever. This is also called censoring the data and when data is censored, we lose valuable information. Another complication with increased limits ratemaking is that data at higher limits may be sparse and cause volatility in results.

Anyway, if we return to the original claims of $2,000 and $4,000 and assume these are the only 2 claims in the data then the Limited Average Severity or LAS at the basic limit 50k is $3,000:

• LAS(50k) = $3,000

Let's suppose Alice's company also has 2 other customers who have a policy limit of 100K and they submitted claims as follows:

• claim #3: $60,000
• claim #4: $70,000

The average severity for all 4 claims is $34,000 so:

• LAS(100k) = $34,000

And the Increased Limit Factor or ILF for the higher 100k limit is:

• ILF(100k)   =   LAS(100k) / LAS(50k)   =   $34,000 / $3,000   =   11.33

The formula is intuitively obvious. In general, if B denotes the basic limit and H denotes the higher limit then:

ILF(H)   =   LAS(H) / LAS(B)

In this example it was easy to calculate LAS(H) and LAS(B) because they were simple averages of the given uncensored data, but this isn't always the case. It depends very much how the data is stored in the database. If we simply had a listing of all uncensored claims, we could use the above method. Often however, claims are censored at the policy limits and we'll look at an example of that further down.

Before moving on, there are a few assumptions you should probably be aware of:

Assumption 1: The ILF formula above assumes:

• all underwriting expenses are variable
• the variable expense and profit provisions do not vary by limit

Assumption 2: Frequency & Severity

• frequency and severity are independent
• frequency is the same for all limits

Werner uses these assumptions to derive the ILF formula. You can read if you want to but it should be enough to be aware of the assumptions and know how to do the calculation. Note that customers who select higher policy limits when they purchase their policy often have lower frequency. That implies that frequency and severity are not independent. A possible reason is that customers who choose higher limits are more risk-averse (they are willing to pay more for insurance protection) and are likely to be more careful drivers.

Example B: Ranges of Uncensored Claims

Werner has a pretty good example of the procedure introduced in the previous example but instead of listing all uncensored claims individually, they are grouped into ranges. Take a few minutes to work through it then try the web-based problem in the quiz.

The first problem in the quiz is practice for the above example.

mini BattleQuiz 2a

Example C: Censored Claims

Friendly warning: For me, this is the hardest problem in the pricing material. I don't know why I had so much trouble with it. Once I figured it out and practiced it a bunch of times I was fine but it just took me a while to get there.

In Example B, the database contained the full loss amounts related to each claim. The amount paid on each claim however depended on the policy limit of the claimant. In other words, the cap due to the policy limits was applied at the very end. Unfortunately, the database usually doesn't contain the full claim amount because the cap due to the policy limit is applied at the beginning. This is what it means to censor the claims. Information is lost and the procedure for calculating ILFs is more nuanced.

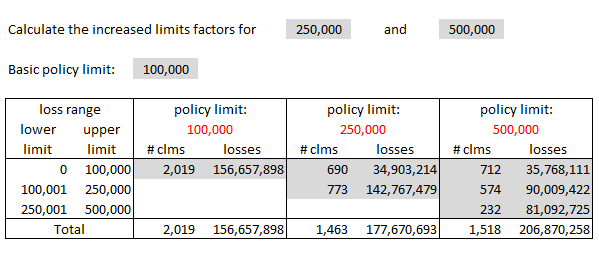
Let's see how to get from the uncensored data provided in Example B to the censored data for Example C as shown below. We'll need a little more information to do this. Example B had 5000 claims altogether but let's suppose that 2,019 of these were on policies with a 100k limit. Since the claims are uncensored, you would also know how these 2,019 claims fell into each range. Let's suppose the distribution is as shown in the table below. You now have enough information to calculate the censored losses for the 100k limit.

You take the losses as given for the 0→100k range but the losses in the higher ranges need to be capped at 100k. The censored losses for the 100k policy limit would be:

• $46,957,898   +   $100,000 x (787 + 282 + 28)   =   $156,657,898

Without going into the remaining calculations, you do the same thing for policy limits 250k and 500k. (The text doesn't provide enough information to be able to do it. They just give you the final result.) The result is a 2-dimensional grid of count and loss information:

Anyway, below is my own version of the text example. I wrote out all the steps in Excel in a way that made sense to me. If you check my solution against the source text, you'll see they didn't actually complete the problem. They stopped after calculating the limited average severities but it was only 1 more simple step to get the final ILFs.

According to Werner, the general idea is as follows:

When calculating the limited average severity for each limit, the actuary should use as much data as possible without allowing any bias due to censorship. The general approach is to calculate a limited average severity for each layer of loss and combine the estimates for each layer taking into consideration the probability of a claim occurring in the layer. The limited average severity of each layer is based solely on loss data from policies with limits as high as or higher than the upper limit of the layer.

You can refer to Werner for further explanation if you'd like but the best way to learn it is just to keep practicing. I also found it helpful to sit in a dark room with my eyes closed and think really hard about the layout of the given information and how all the numbers fit into the solution. Anyway, here's how I did it. Study it and then do the practice problems. The quiz also has a web-based version for an infinite amount of practice.

Here are 4 practice problems in pdf format:

Practice: 4 ILF problems (Censored Data)

Here is a similar problem from the 2019.Fall exam. The data is presented differently from the example above, but it's basically the same problem. The examiner's report uses shortcuts to solve it but if you want to see how to solve it using the method above, the Excel solution is also given below: (Note that I "translated" the given information into a format that matches the above example. You can look at the cell formulas to see how I did this.)

E (2019.Fall #13)

Excel Solution: 2019.Fall #13   ← I translated the given information so that it would fit the format in the above example.

The second problem in the quiz is practice for the above example.

mini BattleQuiz 2b

Miscellaneous ILF Topics

Here are few miscellaneous considerations regarding ILFs. They're easy. Just read them over.

• Development & Trending: Ideally, losses used in an Increased Limits Factor analysis should be developed and trended. Trending is important because recall from chapter 6 that trends have a leveraged effect on losses at higher layers. Development is important because different types of claims may develop differently. An example would be large claims versus small claims. Large claims may also have more volatility since it's more likely for courts to be involved if there is a dispute.

• Sparse Data and Fitted Curves: When performing an Increased Limits Factor analysis, empirical data at higher limits tends to be sparse compared to data at basic limits and this can lead to volatility in the results. One solution is to fit curves to empirical data to smooth out fluctuations. According to Werner:

To calculate LAS(B), Limited Average Severity at the basic limit, just substitute B for H. Then ILF(H) = LAS(H) / LAS(B). You're unlikely to asked this on the exam, but memorize the formula just in case. It's a calculus exercise. Common distributions for f(x) are lognormal, Pareto, and truncated Pareto.

• Multivariate Approach: A multivariate approach to increased limits (such as GLMs) does not assume frequency is same for all sizes of risk and this is an advantage. For example, frequency may actually be lower for higher policy limits. This may be because customers who buy higher limits are more risk-averse and take other steps to mitigate losses. For that reason results are sometimes counter-intuitive. We could have H₁ < H₂ but ILF(H₂) < ILF(H₁). Just something to keep in mind.

The last few BattleCards in this quiz cover these concepts.

mini BattleQuiz 2c

Deductible Pricing

Intro to Deductibles

A deductible is the amount the insured must pay before the insurer's reimbursement begins. For example if an insured has a collision causing $700 of damage and their policy deductible is $250, then the insured is responsible for $250 while the insurer pays the remaining $450 (subject to applicable policy limits.)

The $250 was a flat-dollar deductible, but the deductible can also be expressed as a percentage although this isn't common with auto policies. If a home insured for $300,000 has a 5% deductible then the insured would be responsible for the first $15,000 of loss. Easy.

Question: identify advantages of deductibles [Hint: PINC]

Premium reduction (for insured)

Incentive to mitigate losses (by insured)

Nuisance claims are eliminated (insurer saves on LAE costs)

Catastrophe exposure is controlled (for insurer)

The calculation problems on deductibles are easier than the problems on ILFs and have been asked far less frequently on prior exams. If you know the basic formulas you can usually figure out how to do the problem. This section should take much less time to study than the ILF section.

Example A: Given Ground-Up Losses

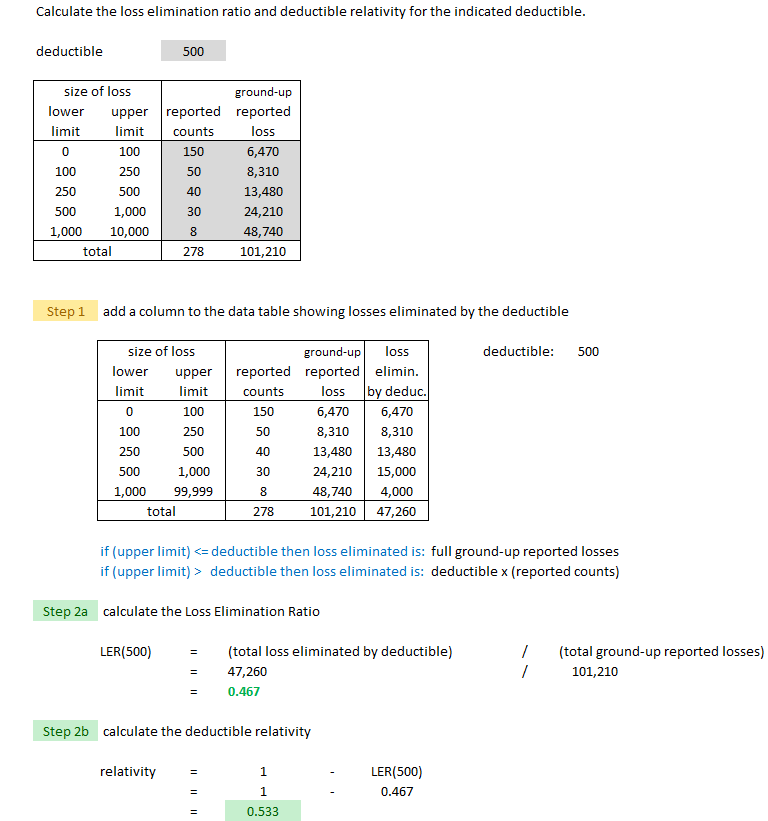
Deductible relativities are typically calculated using a loss elimination ratio or LER. If D is the deductible amount then LER(D) is the loss elimination ratio for deductible D. The text derives the following formula:

LER(D)   =   (losses eliminated by deductible) / (ground-up losses)

The derivation assumes all expenses are variable and that the variable expenses and profit are a constant percentage of premium. I don't think the derivation is important but keep in mind the assumptions. Once you've got the LER, calculating the deductible relativity is easy:

deductible relativity   =   1 – LER(D)

Below is an example Alice worked out that is similar to example from the text. A key observation is that you're given ground-up losses. That means if an insured has an accident causing $700 worth of damage and their deductible is $250, the insurer would record $700 of ground-up losses in their database even though they pay only $450 in net losses. It also means that if the accident caused only $200 worth of damage, the insurer would still record have a record of the $200 ground-up loss even though their net loss is 0. This is similar to censored versus uncensored losses in the ILF procedure.

The first calculation problem in this quiz has a similar web-based problem for practice.

mini BattleQuiz 3a

Example B: Given Net Losses

In the previous example you were given ground-up losses but this is often not available for deductible data. It was similar with ILFs. The ILF procedure was much easier when you had uncensored data versus censored data but it's more likely for an insurer's loss database to have only censored ILF data. With deductibles, the insurer likely records only net losses. For insureds with a deductible of $250, the insurer would have no idea how many accidents there were where the total damage was less than $250.

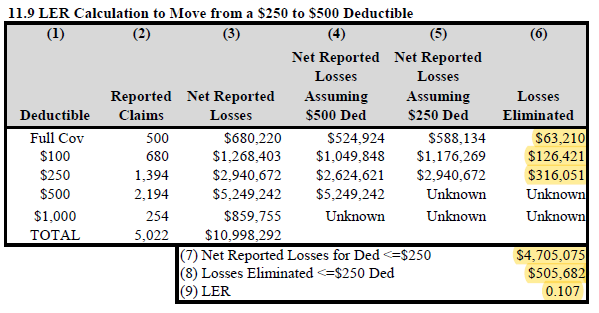
The example below is from the text and shows how to calculate the LER when moving from a $250 deductible to a $500 deductible.

Deductibles: to find losses eliminated when changing from deductible D1 to D2, use only data on policies with deductibles ≤ D1

For this example, this means we can only use data on policies with deductibles ≤ $250. The highlighted values are the only values you have to calculate. Everything else is given.

The second web-based problem in this quiz provides more practice calculating the deductible relativity using net losses rather than ground-up losses.

mini BattleQuiz 3b

Miscellaneous Deductible Topics

• Development & Trending: Losses used in a deductible pricing analysis should be developed and trended just as with Increased Limits Factors. Trending is important because recall from chapter 6 that trends have a leveraged effect on losses at higher layers. Development is important because different types of claims may develop differently.

• Sparse Data and Fitted Curves: A deductible analysis can also be performed with curves fitted to empirical data to smooth out fluctuations. The formula is very similar to the versions used for increased limits:

I think a calculation using this formula is unlikely to come up on a computer-based exam (because it requires integration) but you should be aware of it as an alternate method for deductible pricing.

• Implicit Assumptions:

→ The LER approach to deductible pricing assumes claiming behavior is the same for each deductible but this probably isn't accurate. For an accident with $1,100 of damage, an insured with full coverage would be more likely to report the claim to their insurer than an insured with a $1,000 deductible. The insured with the $1,000 deductible would only receive $100 and their premium rates may also increase which could negate the benefit of the $100 reimbursement.

→ Low-risk insureds tend to select higher deductibles and overall tend to have fewer accidents. The LER doesn't account for this so different deductible levels may not be properly priced. Methods from Werner09.RiskClass and Werner10.Multivariate can account for this however.

→ The LER approach determines a percentage credit and this can have an unintended effect. For example, suppose the credit for moving from a $0 deductible policy to a $250 deductible policy is 15%. If a $0 deductible policy with a premium of $2,000 moves to a $250 deductible policy, it would receive a premium reduction of $300. The insured comes out at least $50 ahead, even if they have an accident and have to pay the deductible. There would be no reason to pay the higher premium for the full coverage policy. To guard against this, insurers sometimes put a cap on the amount of dollar credit from the deductible.

Size of Risk for Worker's Compensation

Intro to WC

Many commercial lines have simple rating algorithms. Workers compensation for example has historically not accounted for the size of insured company. There are 3 ways this can be addressed:

• vary the expense component for large risks
• incorporate premium discounts
• incorporate loss constants

These may be used individually or in combination.

Premium Discount (Expense Components)

Commercial lines insurers typically use the "All Variable" expense method. Both small and large insurers pay the same percentage of premium for expenses. But some expenses (Ex: cost of printing policy forms) are fixed so small companies are undercharged and large companies are overcharged. There are 3 ways this inequity in the expense component can be addressed:

• apply the variable expense provision only to the first $x of premium
• charge an expense constant to all risks
• apply a premium discount to policies with premiums higher than a certain dollar amount

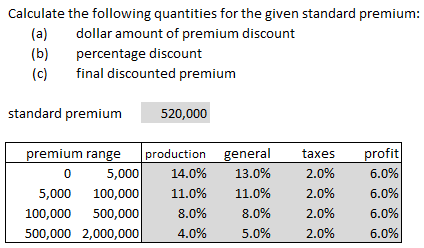
Only the premium discount calculation is discussed further in the text. The idea is that production expenses and general expenses should be a lower percentage of premium for higher premium policies. In other words, there is a graduated expense discount scale applied to the premium in different layers as shown in the example below. Note that taxes and profit do not vary with premium.

The calculation as shown in the example below is mostly self-explanatory. You're asked to calculate 3 different quantities but once you have the first one, the premium discount, the other two are simple.

The only mildly tricky aspect of this problem is using the given standard premium to calculate "premium-in-range". This is column (3) in the solution. For this problem, the standard premium is $520,000 and we need to know how much of this premium falls into each of the premium ranges. The trick is to always start at the bottom of the table.

• On the bottom row: how much of the $520,000 falls into the range $500,000 to $2,000,000? Well, it's pretty easy to see that it's $20,000, with $500,000 remaining.
• Moving up to the next row: how much of the remaining $500,000 falls into the $100,000 to $500,000 range? The answer is $400,000, with $100,000 remaining.
• Moving up to the next row: how much of the remaining $100,000 falls into the $5,000 to $100,000 range? The answer is $95,000, with $5,000 remaining.
• On the top row: how much of the remaining $5,000 falls into the $0 to $5,000 range? The answer is $5,000, with $0 remaining.

And here is the solution:

The first calculation problem in this quiz is a web-based problem for more practice on calculating the premium discount.

mini BattleQuiz 4a

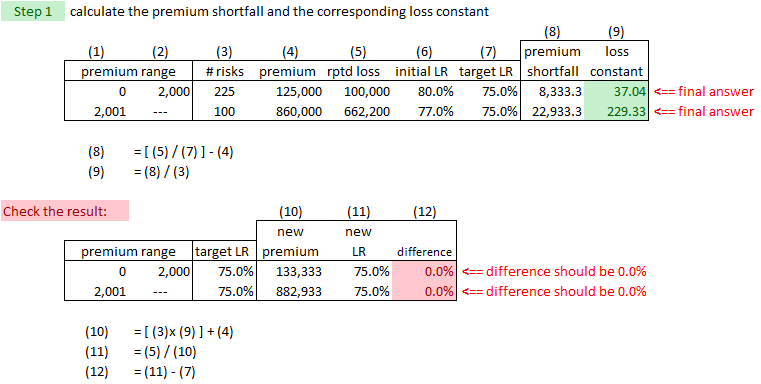
Loss Constants

In the previous section, we used different expenses for different premium ranges. Expected losses are also often different for different premium ranges. In particular, smaller insureds, which fall into lower premium ranges, often have worse loss experience. There are a few potential reasons for this:

• small companies have less sophisticated safety programs (such programs are expensive)
• small companies lack injury rehabilitation programs (injured workers stay out longer)
• small companies are less impacted by experience rating (less incentive to mitigate losses and maintain good loss experience)

Traditionally, a loss constant has been added to the premium to equalize the final expected loss ratios between small and large insureds.

The target loss ratio for both small and large insureds is 75.0% so both will require a loss constant added to the per-risk premium to bring their current loss ratios down to the target level. Note that the current loss ratio for the small insured at 80% is indeed worse than that for the large insured at 77%. Here's the solution.

Alice also included a check to make sure the loss constant does indeed accomplish its purpose. Double-checking your work is another awesome "pro tip" from Alice!

The second calculation problem in this quiz is a web-based problem for more practice on calculating loss constants.

mini BattleQuiz 4b

Insurance to Value (ITV)

Intro to ITV

Suppose there are 2 homeowners and the values of their homes are $250,000 and $200,000. When they go to buy property insurance it would make sense for them to each buy a policy with an Amount of Insurance (AOI) equal to the value of the home. That way, if they suffer a total loss they will be fully reimbursed. The problem is that the greater the AOI written into the policy, the higher the premium. The homeowner with the $250,000 house may want to save money by purchasing a policy with an AOI less than the full $250,000 replacement cost. This is where the concept of Insurance to Value comes in:

Definition: Insurance-to-Value indicates how the level of insurance chosen relates to the overall value or replacement cost of the item

That's the definition provided in the source text. Alice likes to think of it as the ratio of AOI to replacement value. When AOI equals replacement cost, we say the item (house, jewelry, etc...) is insured to full-value. If a homeowner does not insure their property to full value, this might seem like the homeowner's personal business. Why would the insurance company care? Well, it turns out that when some homeowners are under-insured while other are fully insured, the homeowners that are under-insured are likely to be charged a premium that is too low. It isn't obvious why this is true however. We'll have to look at a detailed example.

Example A: Both Homes Insured to Full Value

This example is easy. Suppose:

• Two homes worth $250,000 and $200,000 are each insured for the full amount
• Expected claim frequency is assumed to be 1% for both homes
• Expected losses are uniformly distributed

It's pretty easy to see that for the $250,000 home:

• average severity   =   $125,000
• pure premium   =   frequency x severity   =   1% x $125,000   =   $1,250

Since AOI = $250,000 (because it's insured to full value), the premium rate per $1,000 of coverage is:

→ $1,250 / ($250,000 / $1,000)   =   $1,250 / 250   =   $5.00

If we do a similar calculation for the $200,000 home, which is also insured to full value, we have:

• average severity   =   $100,000
• pure premium   =   frequency x severity   =   1% x $100,000   =   $1,000

The premium rate per $1,000 of coverage is:

→ $1,000 / ($200,000 / $1,000)   =   $1,000 / 200   =   $5.00

You get the same premium rate per $1,000 of coverage for both homeowners, assuming no expenses or profit. If each homeowner is charged $5.00 per $1,000 of coverage, their total premium will cover their expected losses. This will not be true however if one of them is under-insured. You'll see why in the next example.

Example B: One Home not Insured to Full Value

We'll do the same calculation as in the previous example except that the $250,000 homeowner only carries AOI = $200,000:

Alice's solution below is a little simpler than the solution provided in the text. (The source text divided the $250,000 loss range into 10 intervals instead of just 2, but you get the same answer.)

The difference here versus the previous example is that the homeowner's payments are capped at $200,000. Even if the homeowner suffers a loss greater than $200,000 the maximum payment is $200,000. This results in a rate per $1,000 of coverage of $6.00 versus only $5.00 when they were insured to full value. This $6.00 rate will cover the expected losses. The problem is that if the insurer doesn't know that this homeowner's AOI is less than the full value of the house and charges them only $5.00 per $1,000 of coverage, the insurer will lose money.

Key Concept: The insurer cannot charge the same rate per $1,000 for all insureds unless all insureds carry the same level of insurance-to-value

Note that the level of insurance-to-value doesn't have to be full value. It just has to be the same value for all insureds. Of course for a company with many homeowners policies, the ITV level will certainly vary among insureds and the insurer must have a way to account for this in the pricing. We'll look at how this is done in the next section. The first calculation problem in the quiz has a very basic web-based problem on calculating the premium rate per $1,000 of coverage.

mini BattleQuiz 5a

Example C: Coinsurance

This is the whole idea behind coinsurance:

Concept: A coinsurance penalty clause corrects for inequity caused by two homes being insured to different levels of ITV by adjusting the indemnity payment in the event of a loss.

Let's now look at the mathematical details of it works...

I found the section on coinsurance in the source text a little confusing. There are a lot of little formulas you have to know and they are presented in an awkward way. For reference, here's the notation you'll need. First the BIG letters:

I:    Indemnity received by the insured after the loss

L:    Loss amount (after deductible)

F:    Face value of policy (AOI)

V:    Value of property

And now the small letters:

c:    coinsurance percentage required

a:    apportionment ratio

e:    coinsurance penalty

I'm not sure why the coinsurance penalty is denoted e. I suppose it's just another one of those mysteries of the universe. Anyway, there are formulas that tie these quantities together and I've written them out in the example below but first let's just talk about what's going on here.

Suppose a homeowner buys a $150,000 insurance policy for their $200,000 house. So F = 150,000 and V = 200,000. The policy wouldn't cover a total loss but maybe the person couldn't afford full coverage. This way, they are at least partially covered. Suppose the homeowner then suffers a $100,000 loss, so L = 100,000.

Question: what indemnity payment would the homeowner receive?

In other words, what is the value of I? Well, since their policy had a face value of $150,000 and the loss was only $100,000, you might think they would be reimbursed the full $100,000 loss. The actual reimbursement however depends on the coinsurance percentage c. Suppose c = 80%. That means the ratio of F to V must be at least 80% to avoid a penalty. In this case F/V = $150,000/$200,000 = 75%, less than the minimum, and the homeowner would indeed be subject to a penalty.

Question: why is the homeowner subject to a penalty on their indemnity payment?

The penalty is to make sure all insureds are treated equitably regardless of their level of insurance.

We know from Example B above that homes insured for less than full value have a pure premium per $1,000 of coverage that's HIGHER than for homes that are insured to full value. Theoretically the insurer could charge a different rate per $1,000 for each insured based on their F/V ratio to make sure rates are equitable. Here, we take a different approach. Instead of charging a higher premium, we apply a penalty to the reimbursement.

Here is the completed version of the above example. The formulas are written out in a step-by-step fashion. Note there are written slightly differently than in the source text. I think (hope?) they are a little clearer this way. The first step is to calculate the apportionment ratio. That's basically the proportion of the $100,000 that the homeowner receives as their indemnity payment.

You now should practice this calculation. The second calculation problem in the quiz is a web-based practice problem just like the example.

mini BattleQuiz 5b

Now that you are familiar with the formulas, there is one more thing we need to cover in this section. It's a visual representation (otherwise known as a graph!) of how the coinsurance penalty varies with the amount of loss. Here's the graph from Werner along with their very nice explanation underneath:

Older exams sometimes asked you to draw this graph. You can't do that in a computer-based exam but here are the key observations you should know:

• the graph starts at the origin
• the maximum coinsurance penalty occurs when L = F (when the Loss amount equals the Face value of the policy)

→ this is the point (F, e_MAX) on the graph

• the penalty then decreases and reaches 0 when L = cV (when the Loss equals the coinsurance requirement dollar-value)

Even though you shouldn't be asked to draw the graph, I could see a question where they give you the graph and ask you to calculate and x-y coordinates, or L-e coordinates, of the point where the coinsurance penalty is at its MAXIMUM and the point where the penalty goes back to 0.

ITV: Mscellaneous

Recall the main concept related to coinsurance:

A coinsurance penalty clause corrects for inequity caused by two homes being insured to different levels of ITV by adjusting the indemnity payment in the event of a loss.

Another way to correct for inequity is to calculate a premium rate based on the level of ITV. That means if 2 homeowners each have a home valued at $200,000, but the first homeowner insures to 90% of the the full value while the second homeowner insures only to 80%, then the second homeowner will be charged a HIGHER rate per $1,000 of coverage. The text lists 2 formulas for this:

If empirical losses are available from an insurer's claims history, we can use this formula:

Otherwise, we need a theoretical distribution of losses f(x), and we use this alternate formula:

This section of the source text also has a bullet point list of "factoids", a favorite type of CAS question. Alice doesn't think it's very likely to be asked but she didn't want to leave it out. We already know that the premium rate per $1,000 decreases as the F (Face value of policy) approaches V (Value of home), but you can be be more specific about this rate of decrease:

Question: how does the rate of decrease of premium rate per $1,000 of coverage depend on the shape of the loss distribution

• Right-skewed distribution (i.e., small losses predominate): the rate will decrease at a decreasing rate as the policy face value increases
• Uniform distribution (i.e., all losses equally likely): the rate will decrease at a constant rate as the policy face value increases
• Left-skewed distribution (i.e., large losses predominate): the rate will decrease at an increasing rate as the policy face value increases

The last important item from here covers different way insurers can encourage customers to properly insure their properties. In other words, to buy a policy with a face value equal to the value of the property. The source text calls these ITV-initiatives.

Question: identify some ITV initiatives

• insurers offer GRC (Guaranteed Replacement cost)

→ allows replacement cost to exceed the policy limit if the property is 100% insured to value

• insurers use more sophisticated property estimation tools

→ so insurers know more accurately whether a property is appropriately insured

• insurers educate customers:

→ coverage is better if F/V is closer to 100% (for both insurer and insureds)

• insurers inspect property and use indexation clauses

→ more information allows insurers to better price a policy

→ indexation clauses ensure the face value of a policy keeps up with the value of the home

• insurers use a coinsurance clause

→ assigns a penalty if the coinsurance requirement is not met

You've already seen the calculation problems in this quiz when you did quizzes 5a and 5b. For the last installment of quiz 5, do the 3 short answer questions.

mini BattleQuiz 5c

Exam Problems

Here are the the remaining old exam problems organized by type of problem...

Increased Limits Factor problems:

mini BattleQuiz 6

Deductible pricing problems:

mini BattleQuiz 7

Insurance-to-Value and coinsurance problems:

mini BattleQuiz 8

And all BattleCards and exam problems together:

Full BattleQuiz You must be logged in or this will not work.

POP QUIZ ANSWERS

MARS or Multivariate Adaptive Regression Spline.

• The MARS algorithm operates as a multiple piecewise linear regression where each breakpoint defines a region for a particular linear regression equation.

Go back