Werner06.LossLAE

Reading: BASIC RATEMAKING, Fifth Edition, May 2016, Geoff Werner, FCAS, MAAA & Claudine Modlin, FCAS, MAAA Willis Towers Watson

Chapter 6: Loss and LAE

Pop Quiz

What is the Fundamental Insurance Equation? Click for Answer

Study Tips

VIDEO: W-06 (001) Loss & LAE → 5:00 Forum

Chapter 6 on Loss & LAE is another long chapter. You have to practice the calculations relentlessly, then memorize (and understand) the non-calculation concepts listed below. There are no shortcuts. Plan to spend significant time here.

There are several different types of calculation problems you need to learn how to do:

adjusting for large individual losses by calculating an excess loss factor
calculating the direct effect of a coverage or benefit level change
adjusting losses from a historical loss level to current loss level (similar to on-leveling of earned premium from Pricing - Chapter 5)
developing of losses to ultimate (this was already covered in Reserving - Chapter 7)
trending losses to a future period (includes selecting a loss trend and calculating the appropriate loss trend period)
calculating basic limits and excess limits loss trends

There also some important non-calculation concepts including:

determining an appropriate shock loss threshold
how to deal with catastrophe losses in a ratemaking analysis
indirect effects of a benefit level change
why trends have a leveraged effect on excess loss severities
the overlap fallacy (trending losses and developing losses are different things)

This is one of the longest chapters on the entire Exam 5 syllabus but if you put the time in now, Pricing - Chapter 8: Indications will go much more smoothly.

Estimated study time: 1 week (not including subsequent review time)

BattleTable

Based on past exams, the main things you need to know (in rough order of importance) are:

loss trend - selecting trends, calculating trend periods for loss trends
trended ultimate loss - development and trending of losses
benefit change

- calculating the direct effect of benefit changes and adjusting losses for benefit changes

- indirect effects of benefit changes

reference	part (a)	part (b)	part (c)
E (2019.Fall #5)	loss trend - AY factor	loss trend - PY factor	overlap fallacy - trend vs development
E (2019.Spring #4)	loss trend - basic limits	loss trend - excess limits	loss trend - total vs basic limits
E (2019.Spring #5)	trended ultimate loss - calculate ¹	excess loss threshold - capping shock losses
E (2018.Fall #5)	loss trend - 2-step procedure
E (2018.Spring #5)	Excel Practice Problems
E (2017.Fall #06)	benefit change - direct effect	benefit change - indirect effect
E (2016.Fall #4)	trended ultimate loss - calculate	impact of a change - lower claim counts	impact of a change - fewer high deductibles
E (2016.Fall #5)	reinsurance - net trended pure premium
E (2015.Fall #4)	loss trend - for pure premium
E (2015.Fall #5)	benefit change - loss adjustment factor	benefit change - loss adjustment factor	loss trend - comment on selection
E (2015.Spring #8)	excess loss - calculate factor	excess loss - calculate ultimate
E (2014.Fall #4)	benefit change - direct effect	benefit change - indirect effect
E (2013.Fall #5)	trended ultimate loss - large loss adjustment	large loss adjustment - appropriate?	rate analysis - suggest modifications
E (2013.Spring #7)	trended ultimate loss - with benefit change
E (2013.Spring #8)	trended ultimate loss - calculate

¹ Sample solution 2 in the examiner's report has errors. For the selected excess loss load, all years are using 169, which is the 2012 value. For the primary losses, the 2012 value of 263,093 is incorrect. It should be 253,967. Then the Total % Excess-to-Primary should be 1.145% (not 1.135%.)

Full BattleQuiz You must be logged in or this will not work.

In Plain English!

Intro to Losses

This intro is almost exactly the same as the intro to Chapter 5 - Premium. In that chapter, we learned how to restate raw premium data from the historical period to the effective period. We did this using the concepts of current rate level, trending, and premium development. In this chapter we're going make analogous adjustments to losses.

Recall the Fundamental Insurance Equation:

premium = (Losses + LAE + U/W Expenses) + U/W profit

This is the insurance version of the basic formula price = cost + profit, where cost equals the term in parentheses. In this chapter, we focus on the Losses portion of the equation. The goal in a pricing analysis is to determine the losses the insurer expects to have to pay out due to future claims. if we simply use raw loss data in our analysis our conclusions may be wrong. Here are 4 specific items that can impact our loss data:

extraordinary losses
coverage and benefit levels
development of losses
trends

Loss Definitions

We covered the basic loss definitions in the reserving material. For a review, including a web-based practice problem, see Reserving Chapter 2 - Basic Formulas. The concepts are the same in the pricing material but there are small differences in terminology between the reserving and pricing source texts:

The dollar-values an insurer pays out can be called either claims (according to the reserving text) or losses (according to the pricing text).
reported loss = (paid loss) + (case reserves)

→ reported loss is the same thing as case incurred loss which is sometimes just shortened to incurred loss

→ case reserves is called case outstanding (or case O/S) in the reserving text

Alice has a quick reminder for you, because it's something you've got to be totally clear on:

for an individual claim:

→ reported loss = (paid loss) + (case reserve)

for a set of claims over a given time period such as a CY:

→ CY reported loss = (CY paid loss) + (change in case reserve)

The change in case reserve is the ending reserve minus the beginning reserve.

(If you're in the exam and you're rushing it's easy to mess this up.)

Loss Data Aggregation Methods

Data aggregation methods have already been discussed. Click the links below for a review.

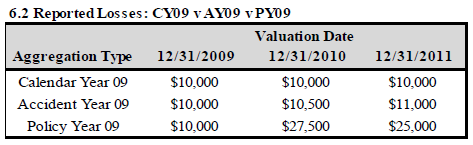
There's a good example from the source text where you're given a claims transactions history and you have to calculate CY, AY, and PY reported losses at 3 different valuation points: 12/31/09, 12/31/10, and 12/31/11. Give it a try. Click for Answer

Common Ratios Involving Statistics

The source text states:

Four common ratios involving loss statistics are: frequency, severity, pure premium, and loss ratio. As stated previously, each ratio is defined by a choice of relevant statistics (e.g., paid or reported losses, or earned or written premium), a data aggregation method (e.g., calendar, accident, policy, or report month/quarter/year), an accounting period, and a valuation date.

We have already covered this material. For a review, including a web-based practice problem, see Pricing Chapter 1 - Basic Insurance Ratios.

Adjustments to Losses: Extraordinary Losses

Large Individual Losses

Large individual losses, also called shock losses, happen infrequently but can cause instability in the ratemaking process. An example may be the permanent disability of a young worker due to complications from COVID-19. A ratemaking analysis using a historical experience period containing a shock loss may suggest the need for a large rate increase, but given the infrequent nature of such losses, it would be better to spread the effect over a longer period to reduce volatility in rates.

Question: what is the general procedure for dealing with shock losses in ratemaking

remove losses above a certain threshold
replace with an average expected large loss amount

Question: how can a shock loss threshold be determined

in general:

• maximize number of losses included

• minimize volatility in the ratemaking process

specific choices may include:

• basic limits amount included in a standard policy

• reinsurance limit

• percentage of coverage amount

• 99th percentile of size-of-loss distribution

• industry benchmark

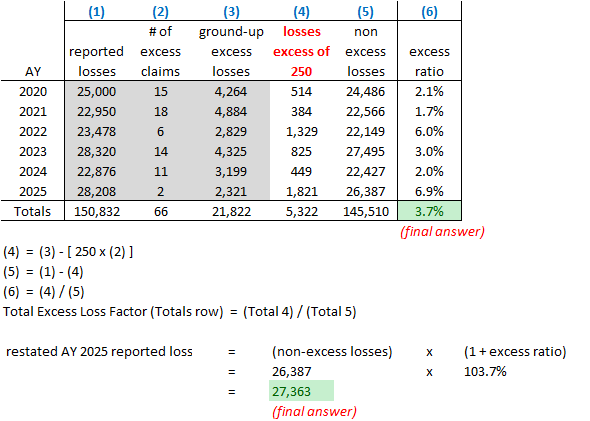
Let's look at a numerical example. As always, we'll start with something very easy then build to something more complex. The key concept is the excess loss factor, also called the excess ratio.

excess ratio = (losses in excess of threshold) / (non-excess losses)

Suppose we have an individual claim of $105,000 and our shock loss threshold is $100,000. Then the excess ratio is 5,000 / 100,000 = 5%. Simple.

Let's now consider the more complex example below where we have many claims across 6 separate accident years and the large loss threshold is 250. The excess loss factor (excess ratio) in column (6) can vary considerably from year to year so we'd like to smooth it using a multi-year average of excess losses. In the example below, the multi-year average is 3.7%. (In practice, the multi-year average should certainly use more than 6 years but the method is otherwise the same.)

The restated AY 2025 reported losses is 27,363. The first 3 shaded columns are the given information and columns (4), (5), and (6) are calculated from the given formulas.

We haven't yet discussed trending for losses, but if you're asked to calculate an excess loss factor and you're also given loss trend information, you should apply the above procedure to trended losses. For future reference, here's a problem where you have to do that. Don't try to do the problem now, we'll cover it later, just be aware that you may have to first trend the losses before applying the excess loss factor procedure.

E (2019.Spring #5)

The quiz has a web-based practice problem in calculating the excess loss factor (without the trending piece).

mini BattleQuiz 1

Catastrophe Losses

Shock losses are individual high severity claims. (See previous section.) Catastrophes are characterized more by a high frequency of claims. The catastrophe itself is a low-frequency, high-severity event but insurers would likely receive many claims across a range of loss levels. Catastrophes refer to natural or man-made disasters such as hurricanes, earthquakes, wildfires, and many others. The total losses from a catastrophe may be high even if individual claims are not.

Catastrophe losses are treated similarly to shock losses. They are removed from the data and replaced with an average expected catastrophe loss amount. There's an example in Appendix B - Homeowners Indication but for now here's an overview.

Question: identify 2 methods of analysis for catastrophe losses in ratemaking

non-modeled catastrophe analysis
catastrophe models

Question: identify scenarios where each type of catastrophe analysis is likely to be used in a ratemaking analysis

non-modeled catastrophe analysis

for events that happen regularly over a period of decades (Ex: hail storms for personal auto)

catastrophe models

for infrequent events with very high total losses (Ex: hurricanes, earthquakes)

Recall that for shock losses, the excess loss factor was calculated as the ratio of (excess losses) to (non-excess losses). A non-modeled analysis works the same way. For the hail storm example, you would calculate the ratio of (hail storm losses) to (non-storm losses) over a 10-30 year period, the time frame being judgmental based on the data. Appendix B - Homeowners Indication discusses a pure premium approach and looks at the long-term ratio of catastrophe losses to exposure.

Pop Quiz A! :-o

If an insurer's concentration of exposures in the most hail-prone area of a region has increased drastically over the past 20 years, would a 10-year or 20-year excess loss average be more appropriate? Click for Answer

A catastrophe model is a stochastic model that estimates the expected annual catastrophe loss based on an insurer's exposure. This amount is then added to the non-catastrophe expected loss to determine the aggregate expected loss used in a ratemaking analysis.

mini BattleQuiz 2

Reinsurance

The topic of reinsurance has already been covered in Reserving Chapter 14 - Recoveries. Here's a calculation problem involving reinsurance. You can take a look at it but it involves trending so you might need to come back to it after you've studied the section on loss trends. This problem also refers to direct losses, which in Werner means essentially the same thing as gross losses. An analysis on a direct basis means without the consideration of reinsurance.

E (2016.Fall #5)

Adjustments to Losses: Coverage and Benefit Levels

Direct and Indirect Effects

The goal is to take losses from the historical experience period and restate them to what they would have been in the planned effective period. Recall that in chapter 5 we adjusted earned premiums for rate changes. Here, we adjust losses for benefit level changes. There are 3 methods for doing this:

restate each individual claim from the current benefit level to the proposed benefit level (most accurate but has a high cost)
restate groups of claims using average current and proposed benefit levels for each group (this is the method demonstrated here)
computer simulation: generate simulated loss data under the proposed benefit conditions ← not discussed any further in source text

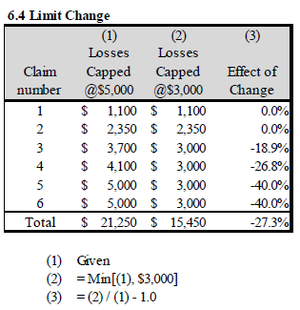
Method 1: (Restate individual claims.) Below is a simple example from the text where an insurer proposes reducing the coverage amount for jewelry, watches, and furs within a standard homeowners policy. The current coverage amount is $5,000 and the proposed amount is $3,000. We have loss amounts for 6 claims, originally capped at $5,000, now capped at $3,000. The aggregate percent change is calculated to be -27.3%. It is very accurate but requires access to individual claim records which can be costly and time-consuming.

The percent change of -27.3% is the direct effect of the coverage change. It assumes no change in policyholder behavior. Some policyholders however may want to retain the higher coverage level by purchasing a Personal Articles Floater (PAF). If the basic homeowners policy is secondary to the PAF, then homeowners losses would be reduced even further. This is an indirect effect. Pay attention to this. The concepts of direct and indirect effects have appeared on the exam. We'll discuss indirect effects in the next example in the context of benefit level changes for worker's compensation.

Method 2: (Restate groups of claims.) The basic version of this type of problem is confusing. That means you have to practice it more than certain other types of problems. It also has a very subtle element to it that is not explicitly discussed in the text but did come up on the 2017.Fall exam. We'll return to this further down. For now, just focus on the basic method for calculating the direct effect of the benefit level change. Here's the type of information you'd typically be given for a worker's compensation example (WC).

Ok, the first thing you have to do is try to make sense of the data:

The Statewide Average Weekly Wage, or SAWW, is easy. It's just the overall average pay for the group of workers in the entire program.
For the table on the left, you have to understand what the ratio to SAWW means. If a particular worker has a wage of $1350 then their ratio to SAWW is 1350/1500 or 90%, putting them in the row labelled 75%-100%. They would be one of the 95 workers within that range of income, and the total income for all those workers $137,750. Maybe it's just me (and Alice) but using percentages seems like a strange way to label the rows. Why not denote the range with the equivalent dollar-values: 75% x $1500 = $1125 and 100% x $1500 = $1500. Anyway, the point is that however you do it, you have to subdivide the workers into a small number of groups; then do the math for the averages of each group. (This avoids the problem with Method 1 where you had to treat each claim individually.)
The table on the right shows current and proposed percentages for 3 specific items, and this is the part I find the most confusing. The standard compensation rate of 80% of pre-injury wages is not changing - the current and proposed percentages are the same. The part that's changing is the increased minimum benefit (from 50% of SAWW to 75%) and the decreased maximum benefit (from 125% of SAWW to 100%). The solution shown below is not long, but it's easy to mess up. You have to be exceedingly careful to put these current and proposed percentages in all the correct places. The first few times you do this problem will be like following a recipe you don't understand. If you work slowly however, and think carefully about what you're doing, it will gradually make more sense.

Below is the solution but I suggest focusing first on step 3 because the formula for that step demonstrates clearly what you're trying to calculate. If you have total current benefits of $465,075 and total proposed benefits of $528,950 then the direct effect of the benefit level change is:

→ (total proposed benefit) / (total current benefit) – 1 = $528,950 / $465,075 – 1 = 13.7%

Now just fill in the details by working backwards through step 2 and then step 1. Of course when working these types of problems yourself you have to do the steps in order, but when you're learning it's often easier to see the bigger picture by starting at the end. (Shout-out to George Polya, famous mathematician, for writing the classic How to Solve It way back in 1944! Good problem-solving never goes out of style.)

Alice's tips: The 4 values calculated in step 1 are used in step 2 to get columns (6) and (7). These columns are calculating the current and proposed benefits for each wage range. Both the current and proposed benefits are 80% of the pre-injury wage which would be easy to calculate, but the benefits are also subject to the given minimums and maximums. That's the part that makes it all so confusing. Side Note: I tried to correct the statement of the problem as given in the examiner's report by altering the range boundaries (see Benefit Changes: Range Boundaries) but in doing I inadvertently made the numbers internally inconsistent. In particular, the 4th row labelled 125% - 156.25% shows 50 workers with total wages of only $87,500. The issue is that if all 50 workers earned the minimum of SAWW x 125% = $1,500 x 125% = $1,875, then their total wages would be 50 x $1,875 = $93,750. So given value of $87,500 in that column is too low and not consistent with the other information given. You can still apply the same method however.

Here's a link to the exam problem similar to the above example as well as 4 similar practice problems. But before you jump in, remember I said this method has a very subtle element to it that is not explicitly discussed in the text but did come up on the 2017.Fall exam. If you want to read more about that click for Benefit Changes: Range Boundaries.

E (2017.Fall #06)

Practice: 4 Benefit Change problems (like 2017.Fall #6)

Part (b) of the exam question above asks for potential indirect effects of the benefit changes. Let's first define that concept.

Question: define the concept of indirect effect of a coverage or benefit level change

a indirect effect arises from changes in claimant behavior due to the coverage or benefit level change

In the exam question, the minimum benefit was increased and the maximum benefit was decreased. How can this change a claimant's behavior?

the increase in minimum benefits affects lower wage workers

→ these workers may then be more likely to make a claim

→ the duration of time out of work may also increase

→ these indirect effects would increase the impact of the benefit change beyond the direct effect calculated in part (a)

the decrease in maximum benefits affects HIGHER wage workers

→ these workers may then be less likely to make a claim

→ the duration of time out of work may also decrease

→ these indirect effects would decrease the impact of the benefit change beyond the direct effect calculated in part (a)

Whenever possible, the actuary should consider these indirect effects. Remember, the key is to ask yourself how the change could affect a claimant's behavior.

Adjusting Historical Loss Data to Current Loss Level

Above, we learned how to calculate the direct effect of the benefit change. The second step is adjusting historical losses to current loss level or CLL. This works exactly the same way as adjusting earned premiums to current rate level. You can glance back at Basic CRL Calculation which shows the formulas for CRLF_CY (Current Rate Level Factor) and EP_CY @ CRL. Bringing losses to current loss level however is generally simpler than bringing premiums to current rate level, and does not involve the parallelogram method.

Triggers: Premiums need to be brought to current rate level when there have been rate changes. ← very common Losses need to brought to current loss level when there have been benefit changes. ← not as common

The analogous formulas for losses are as shown below. You simply replace EP with Loss and CY with AY:

Loss_AY = Losses for accident year AY (unadjusted loss data)

Loss_AY @ CLL = Loss for accident year AY at Current Loss Level

CLLF_AY = Current Loss Level Factor for accident year AY

Then

Loss_AY @ CLL = Loss_AY x CLLF_AY

The formula for the CLLF_AY terms is :

CLL = Current Loss Level

ALL_AY = Average Loss Level for accident year AY

CLLF_AY = CLL / ALL_AY

Let's look at a few examples where these formulas are used...

E (2015.Fall #5) Parts (a) and (b) of this old exam problem demonstrate the calculation. It's a good problem and the examiner's report solution is very well explained. Before you look at it, here a few things to keep in mind:

This problem uses accidents quarters rather accident years (or calendar years if it were premiums) but you should be able to follow the solution. Instead of a square with area = 1.0 representing accident years, you have tall thin rectangles of area = 0.25 representing accident quarters. You just have to be a little more careful when calculating the geometric areas of the resulting polygons.
The benefit change may only affect policies written on or after the date of the benefit change or all policies in-force on that date. This is analogous to rate changes (which affect only new policies) or law changes (which affect all polices in-force). The first case is represented geometrically by a diagonal line in the diagram and the second by a vertical line. Conceptually there is no difference. It's only the shapes of the areas that change.

You may need to return to part (c) later because it involves loss trending which we haven't covered yet.

There's a link below to 3 pages in the source text with another good example. The sentence where it begins is highlighted near the top of the first page.

EXAMPLE: Current Loss Level Adjustment Factors

And the quiz...

mini BattleQuiz 3

Adjustments to Losses: Development

The development method for estimating ultimate losses is discussed in detail in the reserving material in Reserving Chapter 7 - Development Method. Note that the pricing text refers to the development method as the chain ladder method.

Adjustments to Losses: Trending

Understanding trending for losses is similar to trending for premiums. If you've got the hang of premium trending, you'll grasp loss trending fairly quickly.

Loss trends consider several factors. Inflation is one, and it usually results in a positive trend. Safety improvements generally lead to a negative trend. Changes in the mix of business can be either positive or negative. For instance, if an insurer promotes a high-deductible policy, this might lower the frequency of claims but increase their severity. So, it's not immediately clear whether this would reduce the overall pure premium.

It's important to distinguish trending from development. Development focuses on estimating losses that are not yet fully known, often referred to as IBNR (Incurred But Not Reported). This is different from accounting for changes in business mix or inflation, which is what trending aims to capture.

Loss Trend Selection

The text has an example data set where they calculate trends using exponential regression but that's something you would likely not have to do on the exam, even in Excel. You should glance at it though just to get a sense for the layout of the data. Exam problems where you have to select a trend are simpler and we'll look at those further down. In the text example below, they consider pure premium (by quarter) but also frequency and severity separately. (Recall that pure premium is the product of frequency and severity.)

The reason for breaking out frequency and severity separately is to better understand the drivers of the trend. Frequency and severity trends may differ in both magnitude and direction and a single pure premium trend could mask that behavior.

The reason for quarterly data is that it's more responsive when trends are changing, although possibly less stable since quarterly data generally has lower credibility than annual data. There's always a trade-off between stability and responsiveness and the final decision is judgmental. Quarterly data, or even half-year data, can also uncover the effects of seasonality. For example, there could be a trend in winter data that's different from the trend in summer data.

Anyway, here's the text example. They selected -1% for the frequency trend and 2% for the severity trend. They ignored the 20-point, 16-point, and 12-point severity trend, presumably judging there to be a change in trend for more recent periods. This combines into a pure premium trend of 0.99 x 1.02 - 1 = 0.98%.

EXAMPLE: Loss Trend Selection

Here's a pretty easy problem based on the example in the text. You have to fill in the missing values then select trends for frequency, severity, and pure premium. The highlighted cells demonstrate that the annual % changes are calculated using like quarters. (If you had annual data, you could just calculate the the percentage change in successive rows of the data table.)

mustard highlights: 3.25% ~ 0.0103 / 0.0100 (excuse the rounding, the frequency values don't quite show enough decimal places)
pumpkin highlights: 4.90% ~ 11.67 / 11.13

Click for Answer

Werner06 (045) loss trend selection problem.png

Let's now look at the trend selection piece of a couple of exam problems...

E (2019.Spring #5): You are not given the actual data, only the regression results, and you have to come up with appropriate frequency and severity trends. The trend selection is part of a larger problem where you have to calculate the trended ultimate loss to be used in a rate indication but we'll get to that later.

Here's what you're supposed to notice:

the frequency trend is stable

→ pick something in the middle like 1.5%

the severity trend seemed stable for the 20, 16, and 12-point fit but something obviously changed for the 8, 6, and 4-point fit

→ a 2-step trend is appropriate here and a reasonable selection is 5.0% for step 1, and 0.0% for step 2 (see examiner's report for other acceptable selections)

You would then use these selections to calculate trend factors based on the appropriate trend periods for the dates provided.

E (2018.Fall #5): Here again you have to come up with appropriate frequency and severity trends, and decide whether to use 1-step or 2-step trending.

Werner06 (052) loss trend selection (18 F 05).png

Here's what you're supposed to notice:

the severity trend is stable

→ pick something in line with the given values, say 5.0%

the frequency trend is not stable so we probably need 2-step trending

→ it's hard to see what's going on just by looking at the trend fits

→ but you are given the extra piece of information (highlighted) about the U/W change on July 1, 2017 and that it materially changed the mix of business

→ from the data table, you can see that July 1, 2017 corresponds to the last 2 data points

→ a reasonable step 1 trend is 6% (based on earlier data) and a reasonable step 2 trend is -7% (based on the last 4 points)

So that's the type of analysis you need to be able to do on the exam regarding trend selection. To use these trends to project historical losses, you also need to know how to calculate the appropriate trend period which is the topic of the next section.

Loss Trend Period

When calculating trend periods below, we assume that policies are written uniformly during the effective period (unless otherwise stated.) See E (2013.Spring #8) for an example where this assumption is modified.

Similar to 1-step and 2-step premium trending, there is 1-step and 2-step loss trending. (Click the links in the previous sentence for a review of premium trending.) Recall that to calculate the trend period for 1-step premium trends, we used AWDs (Average Written Dates) but we could also have used AEDs (Average Earned Dates). For loss trends, we use AADs (Average Accident Dates) and that calculation works almost exactly the same way as for AEDs. That means you basically already know how to do it. If you'd like, you can review the web-based problems on premium trend period in Premiums BattleQuiz #4. The first problem shows the premium trend period calculation in terms of both AWD and AED.

For losses, the 1-step loss trend period is the difference between the following 2 AADs (Average Accident Dates). The differences from the AED formulas are shown in red:

AAD for losses during AY historical period = (mid-point of historical period) AAD for losses during PY effective period = (mid-point of effective period) + 0.5 x (policy term)

Notice the first AAD uses an AY historical period for losses whereas for premium trend, we use a CY period for earned premium. The above formulas are a convenience for the exam where speed is important but of course you should understand the logic as well. Let's think through a couple of examples of calculating AADs.

Example A: 1-step trend period with annual policies

Suppose we're given:

historical period is AY 2021 (Jan 1, 2021 to Jan 1, 2022)
planned rate change is Jan 1, 2024 with rates in effect for 1 year (effective period is Jan 1, 2024 to Jan 1, 2025)
policies are annual and written uniformly over time

Then using the formulas:

→ AAD₁ = midpoint of historical period = July 1, 2021

→ AAD₂ = (midpoint of effective period) + 0.5 x (policy term) = (July 1, 2024) + 0.5 x (1 year) = Jan 1, 2025.

→ trend period = AAD₂ - AAD₁ = 3.5 years

Or instead, thinking through the logic:

→ AAD₁: the simple numeric midpoint of the AY 2021 historical period, which is July 1, 2021 (this one is always easy for losses)

→ AAD₂: 1-year policies written uniformly between Jan 1, 2024 and Jan 1, 2025 should have losses spread (roughly) uniformly between Jan 1, 2024 and Jan 1, 2026, and the average accident date for that 2-year range is the simple numeric mid-point which is Jan 1, 2025.

→ trend period = AAD₂ - AAD₁ = 3.5 years (same as with using formulas)

Example B: 1-step trend period with 6-month policies

Same as example 1 except with 6-month policies. Using the formulas:

→ AAD₁ = midpoint of historical period = July 1, 2021 (same as for annual policies)

→ AAD₂ = (midpoint of effective period) + 0.5 x (policy term) = (July 1, 2025) + 0.5 x (½ year) = Oct 1, 2024.

→ trend period = AAD₂ - AAD₁ = 3.25 years

Or instead, thinking through the logic:

→ AAD₁: the simple numeric midpoint of the AY 2021 historical period which is July 1, 2021 (same as for annual policies)

→ AAD₂: 6-month policies written uniformly between Jan 1, 2024 and Jan 1, 2025 should have losses spread (roughly) uniformly between Jan 1, 2024 and Jul 1, 2025, and the average accident date for that 1.5-year range is the simple numeric mid-point which is Oct 1, 2024.

→ trend period = AAD₂ - AAD₁ = 3.25 years (same as with using formulas)

Example C: 2-step trend periods with annual policies

Suppose we're given:

historical period is AY 2021 (Jan 1, 2021 to Jan 1, 2022)
planned rate change is Jan 1, 2024 with rates in effect for 1 year (effective period is Jan 1, 2024 to Jan 1, 2025)
policies are annual and written uniformly over time
plus:

→ an U/W change went into effect sometime during the 4th quarter of 2022 materially changing the composition of the book of business

→ you are given quarterly loss data

Step 1 trend period:

→ AAD₁ = midpoint of historical period = July 1, 2021

→ AAD₂ = midpoint of latest available data period = midpoint of 4th quarter 2022 = Nov 15, 2022

→ trend period = 16.5 / 12 months = 1.375 years

Step 2 trend period:

→ AAD₁ = AAD₂ from step 1 trend peiod = Nov 15, 2022

→ AAD₂ = (midpoint of effective period) + 0.5 x (policy term) = (July 1, 2024) + 0.5 x (1 year) = Jan 1, 2025.

→ trend period = 25.5 / 12 months = 2.125 years

Note the sum of the step 1 and step 2 trend periods equals 3.5 years, which is the same as the total trend period from Example A. It's just that Example C broke that period into 2 pieces due to the mix change in 4th quarter 2022.

Examples A, B, C above were for AY historical periods, but sometimes the historical period is a PY. We already know how to calculate the AAD for policy year however. According to the formula in the box at the beginning of this section:

AAD for PY losses = (midpoint of PY) + 0.5 x (policy term)

Here's a quick tip before you try the old exam problems in the quiz...

Annual versus Quarterly loss data for 2-step trending: → Most of the old exam problems assume you're working with annual data. → That means the latest available data point for 2-step trending is a year. → So the "trend-to" point will be 7/1/20xx (mid-point of year, not 11/15/20xx which would be the mid-point of Q4)

This quiz is fairly long. You might want to do part of it then come back later for the rest.

mini BattleQuiz 4

Leveraged Effect of Limits on Severity Trend

This is a simple concept and you can cover this section in about 30 minutes, including the practice problems linked to below.

In the previous sections, we looked at applying frequency and severity trends to losses in the historical period to bring them to the appropriate cost level in the future effective period. Recall also the discussion of Large Individual Losses and excess loss factors. Often in a ratemaking analysis, we subdivide the raw loss data into basic limits losses and excess limit losses.

basic limits losses are losses that have been censored/capped at a predefined limit referred to as the “basic limit.”
total limits losses are losses that are uncensored (not capped)
excess limits losses = (total limits losses) – (basic limits losses)

The source text has an example demonstrating these concepts using 5 individual claims capped at the basic limit of $25,000 and a total limits loss trend of 10%. Use the given formulas to verify the entries in the table shown a little further down. The key observation is that if the severity trend is recalculated separately on the basic and excess layers you get different answers:

basic limits loss trend = 102,500 / 99,000 = 3.5% ← lowest in magnitude
total limits loss trend = 10% (given)
excess limits loss trend = 39,400 / 30,000 = 31.3% ← HIGHEST in magnitude

Further explanation is provided below the table.

Werner06 (070) excess limits severity.png

Basic limits has the lowest magnitude severity because claims near (but under) the limit will contribute some of their trended losses to the excess layer. For example, consider claim # 3 of $24,000. Applying a 10% trend gives $26,400, but since it's capped at $25,000, the extra $1,400 is dumped into the excess layer. The basic limits layer only gets $1,000 of the total increase. This reduces the effect on the basic limits layer but leverages the effect on the excess layer.

if the total limits severity trend is positive: basic limits trend ≤ total limits trend ≤ excess limits trend

Note that this inequality is reversed if the trend is negative. This is a classic way for examiner's to trick you if you're not careful. The magnitude of the basic limits trend is always the lowest, but if trends are negative, the inequality reads as follows

if the total limits severity trend is negative: basic limits trend ≥ total limits trend ≥ excess limits trend

Before we get to the exam and practice problems, note that similar statements hold for deductibles. Mathematically there is no difference between a limit and a deductible because both are just points where data is subdivided into a lower and higher layer (basic and excess.) In the context of insurance however, deductible and limit have different meanings because the insurer is not responsible for any amounts below the deductible. What you have to understand is that for a given general severity trend, the trend effect on losses above the deductible will be greater than the general trend, just like with the excess layer (layer above the limit.)

Here's an exam problem on leveraged severities with Alice's solution and 2 more practice problems:

E (2019.Spring #4)

Solution: 2019.Spring #4

Practice: 2 Leveraged Severity problems (like 2019.Spring #04)

This quiz is easy if you've done the practice problems above.

mini BattleQuiz 5

Overlap Fallacy

After Ian-the-Intern studied this chapter on loss development and trending, he didn't really understand the difference. It seemed to him that development and trending were doing the same thing. Alice took him aside (poor boy) and explained to him that wasn't the case. He was falling into a trap called the overlap fallacy. But she told him not to feel bad because even actuaries used to fall into that trap. The explanation is simple if you think about it the right way:

trending takes losses at a particular age of development from a historical period cost level to a future period cost level
development takes losses at a particular cost level from an immature age of development to ultimate

You should memorize these bullet points, but of course you have to understand them as well.

For our purposes, trending takes losses from the historical period to the effective period then development takes them from the effective period to ultimate. In this case trending and development apply to distinct time frames. If your historical period is AY 2020 and you're doing your analysis on Dec 31, 2021, then those AY losses are aged 24 months, not ultimate. When you trend them to the future effective period, the trend factor is correcting for inflation and changes in mix of business but they are still aged 24 months. For your analysis however, you need the losses at ultimate so you still have to apply development on top of the original trending.

Loss Adjustment Expenses

Loss Adjustment Expenses or LAE ALAE & ULAE is discussed in detail in the reserving material. When we studied LAE in the reserving context, there was no mention of trending. For ratemaking however, LAE should be trended along with losses.

A Few Extra Exam Problems

POP QUIZ ANSWERS

Fundamental Insurance Equation: premium = (Losses + LAE + U/W Expenses) + U/W profit

Go back

Data Aggregation Example

Here's the summarized answer:

Werner06 (012) claims transaction history answers.png

And here's the detailed explanation from the source text:

EXPLANATION: claims transaction aggregation