Werner09.RiskClass

Reading: BASIC RATEMAKING, Fifth Edition, May 2016, Geoff Werner, FCAS, MAAA & Claudine Modlin, FCAS, MAAA Willis Towers Watson

Chapter 9: Traditional Risk Classification

Pop Quiz

What is the formula for the loss ratio method for calculating an indicated rate change? Click for Answer 

Study Tips

VIDEO: W-09 (001) Risk Classification → 4:30 Forum

Previous chapters looked at an overall indication for a book of business. Different customers should get different rates however, based on factors like where they live and what limits/deductibles they select. This chapter looks at how to segment customers into different categories according to their individual level of risk. This is called classification ratemaking. This chapter has 4 types of calculation problems:

• quantification of the impact of adverse selection
• pure premium method for calculating indicated relativities   ← frequently asked
• loss ratio method for calculating indicated relativities
• adjusted pure premium method for calculating indicated relativities   ← frequently asked

The source text shows how the formulas for the various methods are derived but this is very unlikely to be asked on an Excel-based exam. You should know that the formulas are based on the Fundamental Insurance Equation but beyond that, the main thing is to know how to use them. Exam problems also often have short-answer questions on the selection and evaluation of rating variables and how to address distortions in the results of the various methods.

I don't think this is a very hard chapter. Just practice the web-based templates and do the old exam problems. There isn't very much to memorize.

Estimated study time: 3 days (not including subsequent review time)

BattleTable

Based on past exams, the main things you need to know (in rough order of importance) are:

• PP method - basic pure premium method, advanced premium method where exposures are adjusted for distributional bias
• miscellaneous facts about rating variables

reference	part (a)	part (b)	part (c)	part (d)
E (2019.Spring #10)	PP method (adjusted) - new rating factors
(2018.Spring #10)	Excel Practice Problems
(2018.Spring #11)	Excel Practice Problems
E (2017.Fall #9)	exposure base - select and evaluate	rating variable criteria - social criteria	adverse selection - quantify the effect
E (2017.Spring #6)	calculate profit - for each scenario	implement new rates? - based on cost
E (2017.Spring #7)	PP method - with credibility 1
E (2016.Fall #13)	PP method - with credibility 1	PP method - with no overall change 1	Werner13.Other
E (2015.Spring #13)	rating variable criteria - evaluate rating variable	PP method (adjusted) - with no overall change
E (2014.Fall #9)	calculate profit - for each scenario	describe ultimate impact - of segmentation	adverse selection - possible response
E (2014.Fall #11)	PP method - with credibility 1	PP method - distortion	large loss - how to adjust for
E (2014.Spring #4)	rate proposal 1: - actuary's response	rate proposal 2: - actuary's response	rate proposal 3: - actuary's response	rate proposal 4: - actuary's response
E (2014.Spring #8)	PP method (adjusted) - new rating factors 2,3
E (2013.Fall #10)	PP method - distortion	PP method (adjusted) - new rating factors
E (2013.Spring #11)	rating variable criteria - evaluate rating variable	rating variable criteria - recommendation	PP method - with credibility 1

¹ This problem requires knowledge from Chapter 12 - Credibility.

² There is an error in sample answer 3. The percent change for territory 2 should be -2.2% not +2.2%.

³ Sample answers 1 & 2 in the examiner's report are not correct. There is a brief forum discussion about this.

Full BattleQuiz You must be logged in or this will not work.

In Plain English!

Importance of Equitable Rates

The example of adverse selection in the source text is more complicated than it needs to be to explain the concept. I'd recommend reading Alice's example below first. She's good at boiling a concept down to its essence.   :-)

Suppose you did a ratemaking analysis using the pure premium method and computed an average rate of $500. Does that mean every customer should be charged the same $500? Of course not. This is just the average rate. It needs to be adjusted up or down depending on the risk characteristics of each customer. It might be a good idea to take 5 minutes and review the definitions given in ASOP 12.

Let's say your auto insurance company has a very simple risk classification system where you divide customers into just 2 groups based on where they live: city or rural. Suppose you analyze losses for these groups and find that city drivers have a higher frequency of accidents than rural drivers. Based on the higher frequency, your analysis shows city drivers should be charged a little more than the average, $600, while rural drivers should be charged a little less, $450. Each group by itself would be self-supporting, meaning their premiums would cover their losses plus insurer expenses and profit. This is the way it's supposed to work. It's very important that the difference in risk between the 2 groups is recognized and reflected in the premium charged.

Let's now suppose your company did not recognize this difference and charged all customers, both city and rural, the same $500. Furthermore, suppose your competitor did recognize the difference and charges appropriate rates. What do you think would happen?

• if you charge $500 for the city customers and your competitor charges $600, you would acquire all the city customers because you are underpriced but you would lose money
• if you charge $500 for the rural customers and your competitor charges $450, you would lose all the rural customers because you are overpriced and would make $0 in profit

Meanwhile your competitor now has all the rural customers but since they have priced them correctly, they will make a profit on those customers. They would have no city customers, which is too bad, but they neither lose nor gain for that class of customers. What I'm describing here is adverse selection occurring in your company:

• when an insurer acquires risks that are underpriced and loses risks that are overpriced (or correctly priced) due to not properly recognizing risk differentials between classes

The opposite of adverse selection is favorable selection:

• when an insurer acquires risks that are overpriced (or correctly priced) and loses risks that are underpriced

The example in the source text is good:

• Originally, motorcycle insurers used very simple rating algorithms that did not include any variation based on the age of the operator. The first companies that recognized that the age of the operator is an important predictor of risk implemented higher rates for youthful operators. In order to keep their overall premium revenue neutral, they lowered rates for non-youthful operators. By doing this, the companies were able to attract a large portion of the profitable adult risks from their competitors. Furthermore, those youthful operators who chose to insure with them were written profitably.

Let's return for a moment to the example of adverse selection provided in the source text. There were actually a couple of exam problems based on this example, but once you understand the concept of adverse selection, those exam problems are pretty easy. If you just use basic logic, I think you can figure them out. Here they are:

E (2017.Spring #6)

E (2014.Fall #9)

mini BattleQuiz 1

Criteria for Evaluating Rating Variables

This section has the easiest to remember memory trick of all time...

Question: identify criteria for evaluating rating variables [Hint: LOSS]

Legal criteria:

- must follow all appropriate laws & regulations

- insurance pricing regulations set by state or province and vary greatly from place to place

- most jurisdictions require rates to be "not excessive, not inadequate, and not unfairly discriminatory"

Operational criteria

- objective

- inexpensive to administer

- verifiable

Social criteria

- affordability

- causality

- controllability

- privacy concerns

Statistical criteria

- statistical significance

- homogeneity

- credibility

You just have to memorize this and be able to explain them. The source text has a pretty good discussion that I've linked to below. Good bedtime reading. Note that I listed them in a different order because I wanted the first letter of each to spell LOSS.

TEXT:   Descriptions of Rating Criteria

Here's a easy little quiz to help you get this into your head.

mini BattleQuiz 2

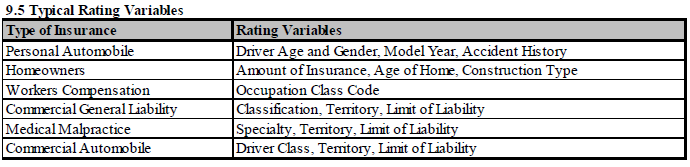
Typical Rating Variables

The source text provides a table showing typical rating variables for common lines of business. I don't think you have to specifically memorize it. Most people know that things like age, territory, and driving record are rating variables for personal auto, and that amount of insurance is a rating variable for homeowners. Take a moment to scan the table and refer back to it when necessary.

Determination of Indicated Rate Differentials

Intro to Univariate Methods

After you've selected rating variables (Ex: location, gender,...) and assigned levels to each (Ex: city & rural for location, male & female for gender) you must also identify the amount of rate variation for each level of each variable. Although a rating variable can have many levels, one level is normally designated as the base level. The rate for all non-base levels is then measured relative to the base level. We'll look at a very basic example of this in the next section.

In this chapter we cover 3 different univariate methods:

• Pure Premium
• Loss Ratio
• Adjusted Pure Premium

A univariate method uses losses for each level of a rating variable in isolation to determine the relativities or differentials. This is in contrast to multivariate methods that consider multiple variables simultaneously and is discussed in Chapter 10 - Multivariate Methods. We also assume in this chapter that the rating algorithm is multiplicative. (Rating algorithms are discussed in detail in "Chapter 2 - Rating Manuals" but that chapter is not on the syllabus.)

The output of these methods is a set of indicated rate relativities.

Pure Premium Approach

Let's return to the example above from the section Importance of Equitable Rates. For this example, I'm making the simplifying assumption here that the pure premium equals the premium charged. In real life, you have to include a provision for expenses and profit but let's ignore that for the moment. In the earlier example, I had told you the appropriate premium rate for city drivers was $600, and for rural drivers, $450. If the overall average rate was $500 then the relativities for the location rating variable are:

• city = $600 / $500 = 1.200
• rural = $450 / $500 = 0.900

It's these relativities that are used to determine the final premium charged.

But let's start from the beginning and suppose you're given:

location	exposures	reported loss
city	100	60,000
rural	200	90,000

The problem is to calculate indicated relativities for the location rating variable. This is a very straightforward univariate analysis. Compute the columns as shown in the table below:

location	exposures	reported loss	pure premium	indicated relativity (normalized)	indicated relativity (rebased to city)
city	100	60,000	600 = 60,000 / 100	1.200 = 600 / 500	1.000 = 1.200 / 1.200
rural	200	90,000	450 = 90,000 / 200	0.900 = 450 / 500	0.750 = 0.900 / 1.200
total	300	150,000	500 = 150,000 / 300	1.000 = 500 / 500	0.833 = 1.000 / 1.200

• pure premium   =   (reported loss) / (exposures)
• indicated relativity (normalized)   =   (pure premium) / (pure premium total)
• indicated relativity (rebased to city)   =   (indicated relativity) / (indicated relativity for city)

The normalized relativities are in the next-to-last column:

• normalized indicated relativity for city   =   1.200
• normalized indicated relativity for rural   =   0.900

The relativities rebased to the base level "city" are in the last column. In this example, the base value for location is "city" and the last column shows rebased relativities measured against the city value which is 1.200.

• rebased indicated relativity for city   =   1.000
• rebased indicated relativity for rural   =   0.750

Ian-the-Intern was initially confused about the difference between normalized and rebased but it's simple if you look at it the right way:

• normalized means relativities are measured against the total row (the relativity for the total row then equals 1.000.)
• rebased means the relativities are measure against base level row (the relativity for the base level row then equals 1.000)

Normalized relativities puts them on a consistent basis, whether that's for a credibility-weighting of 2 sets or relativities (see next section) or for comparison to competitor's relativities. For rebasing, we could just as easily have designated "rural" to be the base level for the location variable. You can check that the new rebased relativities for city and rural are 1.333 and 1.000, and for the total row, 1.111.

The first BattleCard in the quiz has an easy web-based problem for practice with the basic pure premium method. (The second BattleCard is relevant to the next section for quiz 3b.)

mini BattleQuiz 3a

Pure Premium Approach - Distortion

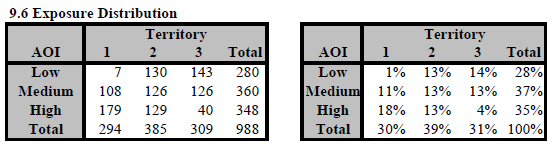
A major drawback of the pure premium method is that the resulting relativities may be distorted from their true values. The "Simple Example" from the source text demonstrates this with exposures for homeowners insurance. (AOI = Amount of Insurance.)

The table on the right shows the percent of total exposures for each cell in the data table. The key observation is that territory 1 has a different AOI distribution from territories 2 and 3. Reading down the columns, territory 1 shows 1%, 11%, 18% which is obviously different from territory 2 which shows an even distribution 13%, 13%, 13%. Territory 3 with 14%, 13%, 4% is the opposite of territory 1 in terms of which AOI is largest and smallest.

This difference in distribution for one rating variable against another is distributional bias.

The text has a very nice explanation for this:

The pure premium for each level is based on the experience of each level, and assumes a uniform distribution of exposures across all other rating variables. To the extent that one territory may have a disproportionate number of exposures of high or low amount of insurance homes, this assumption is violated. By ignoring this exposure correlation between territory and amount of insurance, the loss experience of high or low amount of insurance homes can distort the indicated territorial relativities resulting in a “double counting” effect.

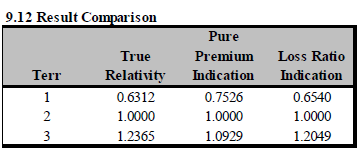
Later in the text, they show a table comparing indicated relativities calculated using the pure premium method to those from the loss ratio method. We'll cover the loss ratio method further down but keep in mind that the loss ratio method is better at handling distributional bias and generally produces results closer to the true values.

Again, the text has a very nice explanation for why the loss ratio method performs better:

Since the pure premium approach relies on exposures (i.e., one exposure for each house year), the risks in each territory are treated the same regardless of the amount of insurance. In contrast, the use of premium in the denominator of the loss ratio reflects the fact that the insurer collects more premium for homes with higher amounts of insurance.

The loss ratio method doesn't produce completely accurate relativities either but that's because the loss ratio method calculates the indicated change from the prior relativities. If the prior relativities are not accurate then the indicated values won't be accurate either. If the prior relativities are accurate then the loss ratio method should work perfectly. The major drawback is that it requires EP @ CRL (Earned Premium at Current Rate Level) and that may not be readily available at the level of individual rating variables.

There is an enhancement however to the pure premium method called the "adjusted pure premium method". This is discussed further down and accounts for distributional bias by adjusting the given exposures in a particular way before applying the pure premium method in the usual way. If this is done, the results will be the same as for the loss ratio method.

The second BattleCard in the quiz gives you practice in identifying when distortion may exist with the basic pure premium method. (The first BattleCard was for the previous section for quiz 3a.)

mini BattleQuiz 3b

Pure Premium Approach with Credibility & Off-Balancing

Some of the exam problems included with this chapter use credibility. That topic isn't discussed until a later chapter but I'm assuming everyone is familiar with the concept of credibility from earlier exams. Here, credibility is calculated using the square root rule. Suppose we're given:

• number of exposures for territory A = 810
• full credibility standard = 1,000 exposures

Then territory A has credibility (810 / 1,000)^½ = 0.9 and that's the weight you would give your indicated relativity for territory A. That's really all you need to know for now. Of course, if the number of exposures for territory A had been greater than 1,000 then territory A would be fully credible and be given a weight of 1.0.

Below is a link to an exam problem using credibility-weighting. You use the pure premium method to calculate the indicated relativities in the usual way but then you have to weight them with the current relativities to get the final credibility-weighted result. (If the problem says the complement of credibility is no change, that's just another way of saying to weight your indicated relativities with the current relativities.)

The other tricky part of this problem asks you to make sure the changes are revenue-neutral. This is also called off-balancing and is discussed much further in Chapter 14 - Implementation. Revenue-neutral means the new relativities do not change the total premium received by the insurer. Another way to say this is that the average premium rate does not change. Some insureds may see a rate increase and others a rate decrease, but the average stays the same. I found the examiner's report solution a little hard to follow, so I've also linked to Alice's solution as well as 2 more practice problems.

E (2017.Spring #7)

Solution: 2017.Spring #7

Practice: 2 Rate Relativity problems (like 2017.Spring #7)

Here's another exam problem using the pure premium method with credibility:

E (2016.Fall #13)

The next quiz just has the 2 exam problems above so you can keep track of them. (Don't forget you can color-code BattleCards by clicking on the leftmost column on any BattleCard page. Then you can filter by color using the BattleCard Filters. There is also a direct link to the filter function under Custom Battles on the BattleActs Main Page.)

mini BattleQuiz 4

Loss Ratio Approach

Do you remember the main difference between the pure premium method and loss ratio method for ratemaking from chapters 7 and 8? The pure premium method calculates an average rate whereas the loss ratio method calculates a rate change. It's similar here. The univariate pure premium method for rate relativities gives you a specific relativity, but the loss ratio method gives you the change from the current relativities. If we use the loss ratio method for a relativity analysis, we need to know the current relativities. That means it cannot be used for a new line of business because there are no current relativities to start with.

The other difference is that the pure premium method uses exposures whereas the loss ratio method uses earned premium, preferably at current rate level. The example below is otherwise not too different from the pure premium example above. Suppose we're given:

location	EP @ CRL	reported loss
city	10,000	12,000
rural	20,000	18,000

Then we calculate the relativities as follows:

location	EP @ CRL	reported loss	loss ratio	change in indicated relativity	current relativity	indicated relativity	indicated relativity (rebased)
city	10,000	12,000	120% = 12,000 / 10,000	1.20 = 120% / 100%	1.000	1.200 = 1.000 x 1.20	1.000 = 1.200 / 1.200
rural	20,000	18,000	90% = 18,000 / 20,000	0.90 = 90% / 100%	0.950	0.855 = 0.950 x 0.90	0.713 = .855 / 1.200
total	30,000	30,000	100% = 30,000 / 300	1.000 = 100% / 100%	--	--	--

So the result is just slightly different from the pure premium method:

• rebased indicated relativity for city   =   1.000
• rebased indicated relativity for rural   =   0.713

Recall that the loss ratio method is better at handling distributional bias than the pure premium method because the loss ratio method uses premiums. As explained earlier, premiums vary according to the level of the rating variable, versus exposures which don't. With exposures, a "high premium" segment of the book of business is counted the same as a "low premium" segment. The implicit assumption in the pure premium method is that exposures within each level of a rating variable are uniform across all other rating variables. If that assumption is violated then the pure premium method may give distorted results.

mini BattleQuiz 5

Adjusted Pure Premium Approach

The loss ratio method requires EP @ CRL for each level of the variable being analyzed but premiums at this level of refinement are often not available. To reduce the impact of distributional bias associated with a univariate approach we will focus on an enhancement to the pure premium method.

Question: how can the pure premium method for relativity analysis be adjusted to reduce distributional bias

• adjust exposures by the exposure-weighted average relativity of all other variables

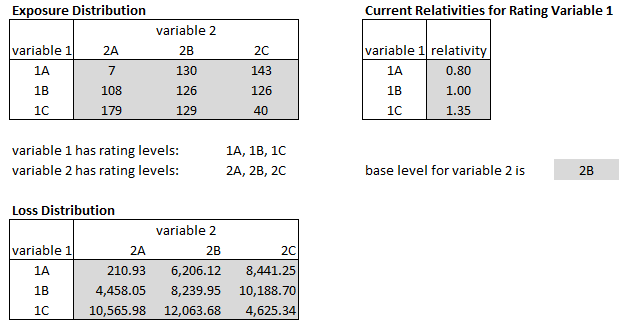
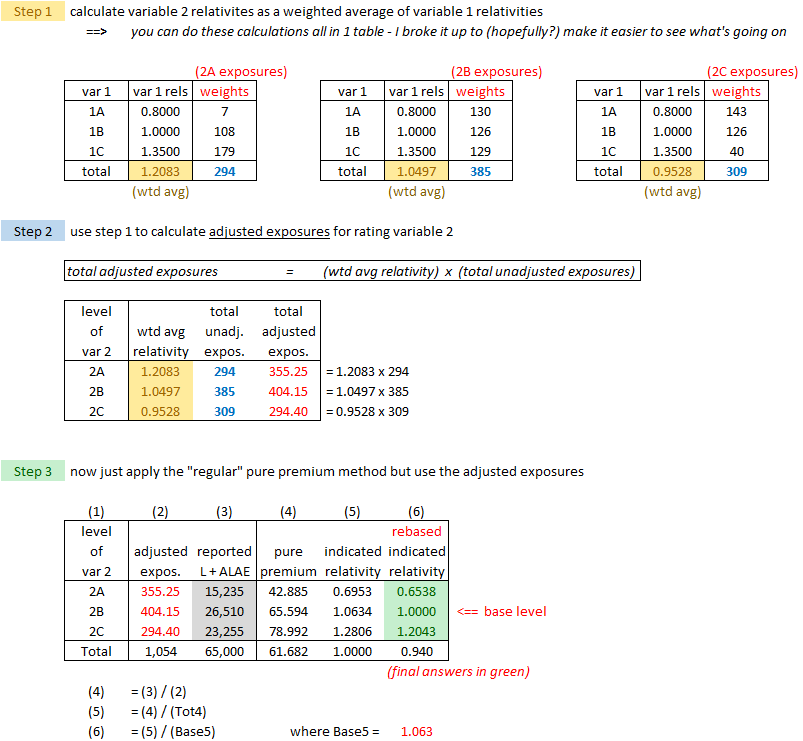
Once you've done this, the pure premium method works exactly as before. Let's see how this works. Below is essentially the example from the source text but I reorganized it a little bit and renamed the rating variables to "variable 1" and "variable 2". (The text uses "Amount of Insurance" and "Territory" for its 2 variables.) Remember the purpose of the adjusted pure premium method is to correct for distributional bias. The loss ratio method already does this but it's often not possible to obtain EP@CRL for smaller segments of data. That's why we need a method based on exposures. Exposures are not affected by rate changes, at least not directly. Study the solution below then do the 4 practice problems.

Problem: Use the adjusted pure premium method to calculate indicated relativities for rating variable 2.

The solution shown below looks more complicated than it really it because I split it into 3 separate steps. In practice you can do all the calculations in 1 table but fair warning: it can be confusing to make sure you're putting all the correct numbers in the correct spots. I personally found it easier to wrap my head around what's going on by breaking it down as shown below. Once you've absorbed it how it works, you can take a few shortcuts.

And here's a link to 4 more practice problems:

Practice: 4 Adjusted Pure Premium Method problems

The quiz has a web-based practice problem for just the exposure-adjustment part of the above problems. It also includes a few old exam problems on the adjusted pure premium method.

mini BattleQuiz 6

Remaining Exam Problems

You can save these for a later review if you'd like...

mini BattleQuiz 7

Full BattleQuiz You must be logged in or this will not work.

POP QUIZ ANSWERS

Loss Ratio method for indicated rate change   =   [ (L + E_L) / P_c   +   F) ]   /   (1.0 – V – Q_T)

Go back